题目内容
4.下列条件:①△ABC的一个外角与其相邻内角等;②∠A=$\frac{1}{2}$∠B=$\frac{1}{3}$∠C;③AC:BC:AB=1:$\sqrt{3}$:2;④AC=n2-1,BC=2n,AB=n2+1(n>1).能判定△ABC是直角三角形的条件有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 根据直角三角形的判定方法,对选项进行一一分析,选择正确答案.
解答 解:①三角形的一个外角与相邻内角相等可以推出这两个角都是直角,所以这个是直角三角形;
②∠A=$\frac{1}{2}$∠B=$\frac{1}{3}$∠C,又∠A+∠B+∠C=180°可以解出∠C=90°,所以它是直角三角形;
③AC:BC:AB=1:$\sqrt{3}$:2,可推出AC2+BC2=AB2,所以它是直角三角形;
④AC=n2-1,BC=2n,AB=n2+1,可推出AC2+BC2=AB2,所以它是直角三角形.
故选A.
点评 本题考查了直角三角形的判定,包括直角三角形的定义和勾股定理的逆定理,解题关键是熟练掌握勾股定理的逆定理以及三角形内角和等知识.

练习册系列答案
相关题目
16.在圆面积公式S=πR2中,变量是( )
| A. | S | B. | S与π | C. | S与R2 | D. | S与R |
13.下列命题中真命题的个数有( )
①小朋友荡秋千可以看做是平移运动;
②两条直线被第三条直线所截,同位角相等;
③过一点有且只有一条直线与已知直线平行;
④不是对顶角的角不相等.
①小朋友荡秋千可以看做是平移运动;
②两条直线被第三条直线所截,同位角相等;
③过一点有且只有一条直线与已知直线平行;
④不是对顶角的角不相等.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
14. 菱形OACB在平面直角坐标系中位置如图所示,点C的坐标是(8,0),点A的纵坐标是1,则点B的坐标是( )
菱形OACB在平面直角坐标系中位置如图所示,点C的坐标是(8,0),点A的纵坐标是1,则点B的坐标是( )
 菱形OACB在平面直角坐标系中位置如图所示,点C的坐标是(8,0),点A的纵坐标是1,则点B的坐标是( )
菱形OACB在平面直角坐标系中位置如图所示,点C的坐标是(8,0),点A的纵坐标是1,则点B的坐标是( )| A. | (4,1) | B. | (4,-1) | C. | (1,4) | D. | (1,-4) |
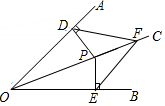 如图,OC是∠AOB的角平分线,点P、F在OC上,PD⊥AO于点D,PE⊥BO于点E,连接DF、EF.求证:DF=EF.
如图,OC是∠AOB的角平分线,点P、F在OC上,PD⊥AO于点D,PE⊥BO于点E,连接DF、EF.求证:DF=EF.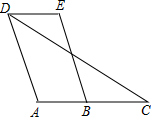 已知:如图,四边形ABCD中,点C在AB的延长线上,连接DC.∠EDC=∠C,AD∥BE.
已知:如图,四边形ABCD中,点C在AB的延长线上,连接DC.∠EDC=∠C,AD∥BE. 如图,在Rt△OAB中,∠ABO=90°,点O与原点重合,OB在数轴正半轴上,∠AOB=30°,AB=2,动点P从原点出发,在数轴正半轴上移动,当△OAP为等腰三角形时,P点表示的数是$\frac{4\sqrt{3}}{3}$或4或4$\sqrt{3}$.
如图,在Rt△OAB中,∠ABO=90°,点O与原点重合,OB在数轴正半轴上,∠AOB=30°,AB=2,动点P从原点出发,在数轴正半轴上移动,当△OAP为等腰三角形时,P点表示的数是$\frac{4\sqrt{3}}{3}$或4或4$\sqrt{3}$.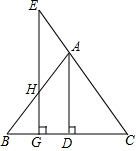 如图,AD是∠BAC的平分线,且垂直于BC,垂足为D,点E在CA上,EG⊥BC,垂足为点G,交AB于点H.写出图中与∠CEG相等的所有角,并说明理由.
如图,AD是∠BAC的平分线,且垂直于BC,垂足为D,点E在CA上,EG⊥BC,垂足为点G,交AB于点H.写出图中与∠CEG相等的所有角,并说明理由.