题目内容
20.为了解某校八年级学生每天干家务活的平均时间,小颖同学在该校八年级每班随机调查5名学生,统计这些学生2015年3月每天干家务活的平均时间(单位:min),绘制成如下统计表(其中A表示0~10min;B表示11~20min;C表示21~30min,时间取整数):| 干家务活平均时间 | 频数 | 百分比 |
| A | 10 | 25% |
| B | a | 62.5% |
| C | 5 | b |
| 合计 | c | 1 |
(2)从上表的“频数”、“百分比”两列数据中选择一列,用适当的统计图表示.
(3)该校八年级共有240学生,求每天干家务活的平均时间在11~20min的学生人数.
分析 (1)根据A的频数和百分比求出总数c,再用总数乘以B的百分比求出a,用C的频数除以总数求出b即可;
(2)选择百分比,画扇形统计图;
(3)用八年级的总人数乘以每天干家务活的平均时间是11~20min的学生所占的百分比,即可得出答案.
解答 解:(1)根据题意得:
c=$\frac{10}{25%}$=40,
则a=40×62.5%=25;
b=$\frac{5}{40}$×100%=12.5%;
故答案为:25;12.5%;40;
(2)根据题意画图如下;
(3)根据题意得:
240×62.5%=150(名).
答:大约有150名学生每天干家务活的平均时间是11~20min.
点评 本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.若分式$\frac{{x}^{2}-1}{x-1}$的值为0,则x的值为( )
| A. | 0 | B. | ±1 | C. | 1 | D. | -1 |
5.观察下列一组图形,它反映了图中点的个数与第n图形之间的某种变化规律,
(1)填写下表:
(2)设第n个图形中点的个数为S个,试写出S与n的关系式S=$\frac{1}{2}$(n+1)(n+2);
(3)求出第10个图形中S的值.

(1)填写下表:
| 第n个图形 | 1 | 2 | 3 | 4 |
| 图中所有点的个数 | 3 | 6 | 10 | 15 |
(3)求出第10个图形中S的值.

10.菱形的一个内角是120°,一条较短的对角线的长为10,则菱形的周长是( )
| A. | 10 | B. | 20 | C. | 30 | D. | 40 |
 如图,AD是△ABC的高,点Q、M在BC边上,点N在AC边上,点P在AB边上,AD=60cm,BC=40cm,四边形PQMN是矩形.
如图,AD是△ABC的高,点Q、M在BC边上,点N在AC边上,点P在AB边上,AD=60cm,BC=40cm,四边形PQMN是矩形.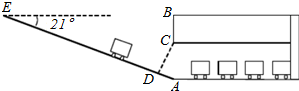 某校九年级数学兴趣小组为了测得该校地下停车场的限高CD,在课外活动时间测得下列数据:如图,从地面E点测得地下停车场的俯角为21°,斜坡AE的长为20米,地面B点(与E点在同一个水平线)距停车场顶部C点(A、C、B在同一条直线上且与水平线垂直)1.6米.试求该校地下停车场的高度AC及限高CD(结果精确到0.1米).(参考数据:sin21°≈0.28,cos21°≈0.91,tan21°≈0.43)
某校九年级数学兴趣小组为了测得该校地下停车场的限高CD,在课外活动时间测得下列数据:如图,从地面E点测得地下停车场的俯角为21°,斜坡AE的长为20米,地面B点(与E点在同一个水平线)距停车场顶部C点(A、C、B在同一条直线上且与水平线垂直)1.6米.试求该校地下停车场的高度AC及限高CD(结果精确到0.1米).(参考数据:sin21°≈0.28,cos21°≈0.91,tan21°≈0.43) 如图,在△ABC中,AB=AC,以AB为直径作⊙O,交BC边于点D,交AC边于点G,过D作⊙O的切线EF,交AB的延长线于点F,交AC于点E.
如图,在△ABC中,AB=AC,以AB为直径作⊙O,交BC边于点D,交AC边于点G,过D作⊙O的切线EF,交AB的延长线于点F,交AC于点E.