题目内容
10. 如图,AD是△ABC的高,点Q、M在BC边上,点N在AC边上,点P在AB边上,AD=60cm,BC=40cm,四边形PQMN是矩形.
如图,AD是△ABC的高,点Q、M在BC边上,点N在AC边上,点P在AB边上,AD=60cm,BC=40cm,四边形PQMN是矩形.(1)求证:△APN∽△ABC;
(2)若PQ:PN=3:2,求矩形PQMN的长和宽.
分析 (1)由四边形PQMN是矩形,得到PN∥BC,即可得到三角形相似;
(2)由三角形相似得到比例式即可求得结果.
解答 解:(1)∵四边形PQMN是矩形,
∴PN∥BC,
∴∠APN=∠B,∠ANP=∠C,
∴△APN∽△ABC;
(2)∵△APN∽△ABC,
∴$\frac{PN}{BC}=\frac{AE}{AD}$,
又∵PQ:PN=3:2,
设PQ=3xcm,则PN=2xcm,
∴$\frac{2x}{40}=\frac{60-3x}{60}$,
解得:x=10,
∴PQ=30,PN=20.
答:矩形PQMN的长和宽分别是30cm和20cm.
点评 本题考查了矩形的性质,相似三角形的判定和性质,熟记相似三角形的判定定理是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.以下说法正确的是( )
| A. | 在367人中至少有两个人的生日相同 | |
| B. | 一次摸奖活动的中奖率是1%,那么摸100次必然会中一次奖 | |
| C. | 一副扑克牌中,随意抽取一张是红桃K,这是必然事件 | |
| D. | 一个不透明的袋中装有3个红球,5个白球,搅匀后想中任意摸出一个球,摸到红球的可能性大于摸到白球的可能性 |
20.为了解某校八年级学生每天干家务活的平均时间,小颖同学在该校八年级每班随机调查5名学生,统计这些学生2015年3月每天干家务活的平均时间(单位:min),绘制成如下统计表(其中A表示0~10min;B表示11~20min;C表示21~30min,时间取整数):
(1)统计表中的a=25;b=12.5%;c=40.
(2)从上表的“频数”、“百分比”两列数据中选择一列,用适当的统计图表示.
(3)该校八年级共有240学生,求每天干家务活的平均时间在11~20min的学生人数.
| 干家务活平均时间 | 频数 | 百分比 |
| A | 10 | 25% |
| B | a | 62.5% |
| C | 5 | b |
| 合计 | c | 1 |
(2)从上表的“频数”、“百分比”两列数据中选择一列,用适当的统计图表示.
(3)该校八年级共有240学生,求每天干家务活的平均时间在11~20min的学生人数.
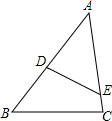 如图,在△ABC中,点D、E分别在AB、AC上,∠ADE=∠C,如果AE=2,AB=3,△ADE的面积是4,则四边形BCED的面积是5.
如图,在△ABC中,点D、E分别在AB、AC上,∠ADE=∠C,如果AE=2,AB=3,△ADE的面积是4,则四边形BCED的面积是5.