题目内容
10.菱形的一个内角是120°,一条较短的对角线的长为10,则菱形的周长是( )| A. | 10 | B. | 20 | C. | 30 | D. | 40 |
分析 首先根据题意画出图形,然后由菱形的一个内角是120°,证得△ABD是等边三角形,继而可得边长等于较短的对角线的长,则可求得答案.
解答  解:如图,∵菱形ABCD中,∠ABC=120°,
解:如图,∵菱形ABCD中,∠ABC=120°,
∴AB=AD,∠A=60°,
∴△ABD是等边三角形,
∴AB=BD=10,
∴菱形的周长是:40.
故选D.
点评 此题考查了菱形的性质以及等边三角形的判定与性质.注意证得△ABD是等边三角形是关键.

练习册系列答案
相关题目
20.为了解某校八年级学生每天干家务活的平均时间,小颖同学在该校八年级每班随机调查5名学生,统计这些学生2015年3月每天干家务活的平均时间(单位:min),绘制成如下统计表(其中A表示0~10min;B表示11~20min;C表示21~30min,时间取整数):
(1)统计表中的a=25;b=12.5%;c=40.
(2)从上表的“频数”、“百分比”两列数据中选择一列,用适当的统计图表示.
(3)该校八年级共有240学生,求每天干家务活的平均时间在11~20min的学生人数.
| 干家务活平均时间 | 频数 | 百分比 |
| A | 10 | 25% |
| B | a | 62.5% |
| C | 5 | b |
| 合计 | c | 1 |
(2)从上表的“频数”、“百分比”两列数据中选择一列,用适当的统计图表示.
(3)该校八年级共有240学生,求每天干家务活的平均时间在11~20min的学生人数.
18.下列三条线段能构成直角三角形的是( )
| A. | 4,5,6 | B. | 1,2,3 | C. | 3,6,9 | D. | 6,8,10 |
18.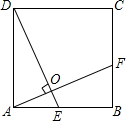 如图,正方形ABCD中,E为AB的中点,AF⊥DE于点O,则$\frac{OE}{BF}$等于( )
如图,正方形ABCD中,E为AB的中点,AF⊥DE于点O,则$\frac{OE}{BF}$等于( )
 如图,正方形ABCD中,E为AB的中点,AF⊥DE于点O,则$\frac{OE}{BF}$等于( )
如图,正方形ABCD中,E为AB的中点,AF⊥DE于点O,则$\frac{OE}{BF}$等于( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{2\sqrt{5}}{3}$ |
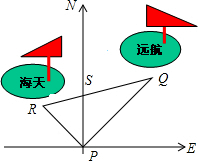 如图,某港口P位于东西方向的海岸线上“远航”号、“海天”号轮船同时离开港口,各自沿同定方向航行,“远航”号每小时航行16n mile,“海天”号每小时航行12n mile,它们离开港口一个半小时后分别位于点Q,R处,且相距30n mile
如图,某港口P位于东西方向的海岸线上“远航”号、“海天”号轮船同时离开港口,各自沿同定方向航行,“远航”号每小时航行16n mile,“海天”号每小时航行12n mile,它们离开港口一个半小时后分别位于点Q,R处,且相距30n mile 把正整数1,2,3,…,按如图所示排列.第1行第1列的数为1,第1行第2列的数为2,第1行第3列的数为6,那么第1行第100列的数为4951.
把正整数1,2,3,…,按如图所示排列.第1行第1列的数为1,第1行第2列的数为2,第1行第3列的数为6,那么第1行第100列的数为4951.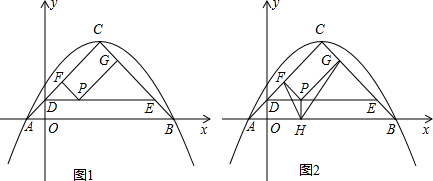
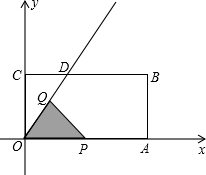 如图,已知矩形ABCD中,OA=8,AB=1,直线y=$\frac{4}{3}$x交BC于D,动点P、Q同时从D出发,点P沿折线OA-AB-BD以每秒3个单位的速度运动到D停止,点Q沿射线OD以每秒1个单位的速度运动,当点P停止时,点Q也停止运动.△OPQ与梯形OABD重叠部分的面积为S,运动时间为t.
如图,已知矩形ABCD中,OA=8,AB=1,直线y=$\frac{4}{3}$x交BC于D,动点P、Q同时从D出发,点P沿折线OA-AB-BD以每秒3个单位的速度运动到D停止,点Q沿射线OD以每秒1个单位的速度运动,当点P停止时,点Q也停止运动.△OPQ与梯形OABD重叠部分的面积为S,运动时间为t.