题目内容
计算:xn+1•xn-1÷(xn+1)2(x≠0)
考点:同底数幂的除法,同底数幂的乘法,幂的乘方与积的乘方
专题:
分析:根据幂的乘方,可得同底数幂的乘除法,根据同底数幂的乘除法,可得答案.
解答:解:原式=xn+1•xn-1÷x2(n+1)
=xn+1+n-1-2(n+1)
=x-2
=
.
=xn+1+n-1-2(n+1)
=x-2
=
| 1 |
| x2 |
点评:本题考查了同底数幂的除法,先利用了幂的乘方,再利用了同底数幂的乘除法,最后利用了负整数指数幂.

练习册系列答案
相关题目
 在如图的直角坐标系中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点),点A的坐标为(-2,3).
在如图的直角坐标系中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点),点A的坐标为(-2,3).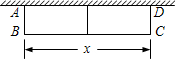 如图,一边利用墙,其余各边用篱笆靠墙围成矩形花圈ABCD,在花圈中间用一道篱笆隔成两个小矩形,墙可利用的最大长度为15m,篱笆总长为24m,设平行于墙的BC边长c m,矩形ABCD的面积为S m2.
如图,一边利用墙,其余各边用篱笆靠墙围成矩形花圈ABCD,在花圈中间用一道篱笆隔成两个小矩形,墙可利用的最大长度为15m,篱笆总长为24m,设平行于墙的BC边长c m,矩形ABCD的面积为S m2.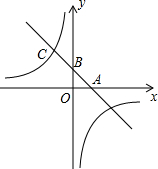 如图,一次函数y=-x+b分别与x轴、y轴交于A、B两点,与反比例函数y=
如图,一次函数y=-x+b分别与x轴、y轴交于A、B两点,与反比例函数y= 如图,⊙O是△ABC的外接圆,AD是⊙O的直径.若OA=6,sinB=
如图,⊙O是△ABC的外接圆,AD是⊙O的直径.若OA=6,sinB=