题目内容
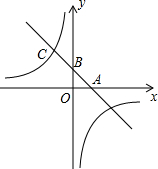 如图,一次函数y=-x+b分别与x轴、y轴交于A、B两点,与反比例函数y=
如图,一次函数y=-x+b分别与x轴、y轴交于A、B两点,与反比例函数y=| k |
| x |
(1)求一次函数与反比例函数的解析式,
(2)根据图象写出,在第二象限内,一次函数的值小于反比例函数的值的x的取值范围.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)把A点坐标代入一次函数解析式可求得b的值,可得到一次函数解析式,则可求得B点坐标,结合中点,可求得C点坐标,代入反比例函数解析式可求得k的值,可得到反比例函数解析式;
(2)可先求得两函数图象另一交点坐标,结合图象可得到一次函数图象在反比例函数图象的下方对应的x的取值,可得到答案.
(2)可先求得两函数图象另一交点坐标,结合图象可得到一次函数图象在反比例函数图象的下方对应的x的取值,可得到答案.
解答:解:
(1)∵一次函数图象过A点,
∴0=-2+b,解得b=2,
∴一次函数解析式为y=-x+2,
∴B点坐标为(0,2),
又B为线段AC的中点,
如图,过点C作CD⊥x轴,

由中位线定理可知CD=2OB=4,
即C点纵坐标为4,又C点在一次函数图象上,
代入可得4=-x+2,解得x=-2,
∴C点坐标这(-2,4),
又C点在反比例函数图象上,
∴k=-2×4=-8,
∴反比例函数解析式为y=-
;
(2)联立两函数解析式可得
,解得
或
,
∴两函数图象的另一交点坐标为(4,-2),
当一次函数值小于反比例函数值时,即一次函数图象在反比例函数图象的下方,
结合图象可知x的取值范围为:-2<x<0或x>4.
(1)∵一次函数图象过A点,
∴0=-2+b,解得b=2,
∴一次函数解析式为y=-x+2,
∴B点坐标为(0,2),
又B为线段AC的中点,
如图,过点C作CD⊥x轴,

由中位线定理可知CD=2OB=4,
即C点纵坐标为4,又C点在一次函数图象上,
代入可得4=-x+2,解得x=-2,
∴C点坐标这(-2,4),
又C点在反比例函数图象上,
∴k=-2×4=-8,
∴反比例函数解析式为y=-
| 8 |
| x |
(2)联立两函数解析式可得
|
|
|
∴两函数图象的另一交点坐标为(4,-2),
当一次函数值小于反比例函数值时,即一次函数图象在反比例函数图象的下方,
结合图象可知x的取值范围为:-2<x<0或x>4.
点评:本题主要考查待定系数法求函数解析式和函数交点,求得C点坐标是求反比例函数解析式的关键,求得另一个交点坐标是(2)的关键.注意数形结合思想的应用.

练习册系列答案
相关题目
为了了解我县参加中考的9500名学生的视力情况,抽查了1000名学生的视力进行统计分析,下面四个判断中,正确的是( )
| A、9500名学生是总体 |
| B、1000名学生是总体 |
| C、1000名学生的视力是总体的一个样本 |
| D、每名学生是总体的一个个体 |
若3x=21,3y=7,则3x-y=( )
| A、7 | B、3 | C、14 | D、21 |
 如图,一次函数y=x+1的图象与反比例函数y=
如图,一次函数y=x+1的图象与反比例函数y= 如图,在△ABC中,∠A=30°,∠ABC=60°,BD是∠ABC的平分线,D在AC上,E是AB的中点,连DE.求证:△ADE≌△BDE.
如图,在△ABC中,∠A=30°,∠ABC=60°,BD是∠ABC的平分线,D在AC上,E是AB的中点,连DE.求证:△ADE≌△BDE.