题目内容
20.一辆出租车从A地出发,在一条东西走向的街道上往返行驶,每次行驶的路程(记向东为正)记录如下(9<x<26,单位:km):| 第一次 | 第二次 | 第三次 | 第四次 |
| x | -$\frac{1}{2}$x | x-5 | 2﹙9-x﹚ |
(2)这辆出租车一共行驶了多少路程?
分析 (1)根据正负数的意义判断即可;
(2)把所行路程相加即可.
解答 解:(1)第1次向东,第2次向西,第3次向东,第4次向西;
(2)因为9<x<26,所以总路程为:
|x|+|-$\frac{1}{2}$ x|+|x-5|+|2(9-x)|
=x+$\frac{1}{2}$ x+(x-5)-2(9-x)
=($\frac{9}{2}$ x-23)(km).
点评 本题考查了整式的加减,掌握正负数的意义以及整式的加减运算法则是解题的关键.

练习册系列答案
相关题目
15.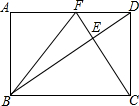 如图,在矩形ABCD中,DC=2$\sqrt{3}$,CF⊥BD分别交BD、AD于点E、F,连接BF.当F为AD的中点时,则BC的长为( )
如图,在矩形ABCD中,DC=2$\sqrt{3}$,CF⊥BD分别交BD、AD于点E、F,连接BF.当F为AD的中点时,则BC的长为( )
 如图,在矩形ABCD中,DC=2$\sqrt{3}$,CF⊥BD分别交BD、AD于点E、F,连接BF.当F为AD的中点时,则BC的长为( )
如图,在矩形ABCD中,DC=2$\sqrt{3}$,CF⊥BD分别交BD、AD于点E、F,连接BF.当F为AD的中点时,则BC的长为( )| A. | 4 | B. | 3$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | 2$\sqrt{6}$ |
9.在${({-\sqrt{2}})^0}$,0,$\sqrt{9}$,$-\frac{π}{3}$,-0.333…,$\sqrt{5}$,3.1415926,0.010010001…(相邻两个1之间依次多1个0)中,无理数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
10.已知$\left\{\begin{array}{l}{x=a}\\{y=b}\end{array}\right.$是方程组$\left\{\begin{array}{l}{11x-13y=15}\\{7x+9y=-25}\end{array}\right.$的解,则下列说法中正确的是( )
| A. | $\left\{\begin{array}{l}{x=a}\\{y=b}\end{array}\right.$是方程11x-13y=15的唯一一组解 | |
| B. | $\left\{\begin{array}{l}{x=a}\\{y=b}\end{array}\right.$是方程7x+9y=-25的唯一一组解 | |
| C. | x=a是方程x+5=0的解 | |
| D. | y=b是方程y-6=-8的解 |
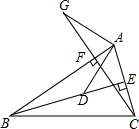 如图,已知在△ABC中,BE、CF分别是AC、AB边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连结AD、AG,则AG与AD有何关系?试证明你的结论.
如图,已知在△ABC中,BE、CF分别是AC、AB边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连结AD、AG,则AG与AD有何关系?试证明你的结论. 如图,AC、BC分别平分∠MAB和∠ABN,∠ACB=90°.
如图,AC、BC分别平分∠MAB和∠ABN,∠ACB=90°.