题目内容
15.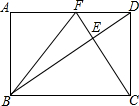 如图,在矩形ABCD中,DC=2$\sqrt{3}$,CF⊥BD分别交BD、AD于点E、F,连接BF.当F为AD的中点时,则BC的长为( )
如图,在矩形ABCD中,DC=2$\sqrt{3}$,CF⊥BD分别交BD、AD于点E、F,连接BF.当F为AD的中点时,则BC的长为( )| A. | 4 | B. | 3$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | 2$\sqrt{6}$ |
分析 根据矩形的性质、同角的余角相等得到∠CDE=∠DFE,得到△DEC∽△FDC;根据DF∥BC,得到$\frac{FE}{EC}$=$\frac{DF}{BC}$=$\frac{1}{2}$,根据相似三角形的性质得到CE•CF=CD2=12,求出CF,根据勾股定理计算即可.
解答 解:∵四边形ABCD是矩形,
∴∠FDC=90°,
∴∠FDE+∠CDE=90°,
∵CF⊥BD,
∴∠FDE+∠DFE=90°,
∴∠CDE=∠DFE,
又∴∠DEC=∠CDF=90°,
∴△DEC∽△FDC;
∵四边形ABCD是矩形,
∴DF∥BC,
∴$\frac{FE}{EC}$=$\frac{DF}{BC}$=$\frac{1}{2}$,
∵△DEC∽△FDC,
∴CE•CF=CD2=12,
∴CF=3$\sqrt{2}$,
∴DF=$\sqrt{C{F}^{2}-C{D}^{2}}$=$\sqrt{6}$,
∴BC=AD=2$\sqrt{6}$.
故选:D.
点评 本题考查的是相似三角形的判定和性质、矩形的性质,掌握相似三角形的判定定理和性质定理是解题的关键.

练习册系列答案
相关题目
20.一辆出租车从A地出发,在一条东西走向的街道上往返行驶,每次行驶的路程(记向东为正)记录如下(9<x<26,单位:km):
(1)说出这辆出租车每次行驶的方向;
(2)这辆出租车一共行驶了多少路程?
| 第一次 | 第二次 | 第三次 | 第四次 |
| x | -$\frac{1}{2}$x | x-5 | 2﹙9-x﹚ |
(2)这辆出租车一共行驶了多少路程?
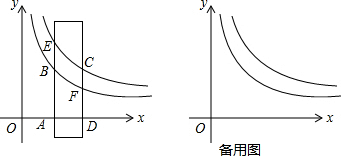
 如图,已知点E,C在线段BF上,BE=CF,∠B=∠DEF,∠ACB=∠F,求证:四边形ABED为平行四边形.
如图,已知点E,C在线段BF上,BE=CF,∠B=∠DEF,∠ACB=∠F,求证:四边形ABED为平行四边形. 为保障北京2022 年冬季奥运会赛场间的交通服务,北京将建设连接北京城区-延庆区-崇礼县三地的高速铁路和高速公路.在高速公路方面,目前主要的交通方式是通过京藏高速公路(G6),其路程为220公里.为将崇礼县纳入北京一小时交通圈,有望新建一条高速公路,将北京城区到崇礼的道路长度缩短到100公里.如果行驶的平均速度每小时比原来快22公里,那么从新建高速行驶全程所需时间与从原高速行驶全程所需时间比为4:11.求从新建高速公路行驶全程需要多少小时?
为保障北京2022 年冬季奥运会赛场间的交通服务,北京将建设连接北京城区-延庆区-崇礼县三地的高速铁路和高速公路.在高速公路方面,目前主要的交通方式是通过京藏高速公路(G6),其路程为220公里.为将崇礼县纳入北京一小时交通圈,有望新建一条高速公路,将北京城区到崇礼的道路长度缩短到100公里.如果行驶的平均速度每小时比原来快22公里,那么从新建高速行驶全程所需时间与从原高速行驶全程所需时间比为4:11.求从新建高速公路行驶全程需要多少小时?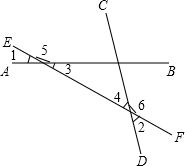 如图所示,直线AB、CD、EF两两相交,若∠1=30°,∠2=60°,则∠3=30°,∠4=60°,∠5=150°,∠6=120°.
如图所示,直线AB、CD、EF两两相交,若∠1=30°,∠2=60°,则∠3=30°,∠4=60°,∠5=150°,∠6=120°. 如图所示,点B,E,F,C在同一条直线上,AF⊥BC于F,DE⊥BC于E,AB∥CD,BE=CF,求证:AB=DC.
如图所示,点B,E,F,C在同一条直线上,AF⊥BC于F,DE⊥BC于E,AB∥CD,BE=CF,求证:AB=DC.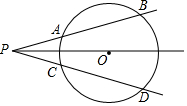 如图,∠P的两边分别与⊙O交于点A、B、C、D,且其平分线恰好过圆心O.求证:PA=PC.
如图,∠P的两边分别与⊙O交于点A、B、C、D,且其平分线恰好过圆心O.求证:PA=PC.