Question

5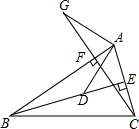．如图，已知在△ABC中，BE、CF分别是AC、AB边上的高，在BE上截取BD=AC，在CF的延长线上截取CG=AB，连结AD、AG，则AG与AD有何关系？试证明你的结论．

Answer 1

分析 结论：AG=AD，AG⊥AD，只要证明△ABD≌△GCA（SAS）即可解决问题．

解答 解：结论：AG=AD，AG⊥AD，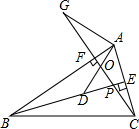
理由是：∵在△ABC中，BE，CF分别是边AC，AB上的高，
∴∠BFP=∠CEP=∠AFO=90°，
∴∠ABD+∠FPB=90°，∠ACG+∠EPC=90°，
∵∠FPB=∠EPC，
∴∠ACG=∠ABD，
在△ABD和△GCA中，
$\left\{\begin{array}{l}{AB=CG}\\{∠ABD=∠ACG}\\{BD=AC}\end{array}\right.$，
∴△ABD≌△GCA（SAS），
∴AG=AD，∠AGC=∠BAD，
∵∠AFO=90°，
∴∠BAD+∠AOF=90°，
∴∠AGC+∠AOF=90°，
∴∠GAD=180°-90°=90°，
∴AG⊥AD．

点评 本题考查全等三角形的判定和性质、同角或等角的余角相等等知识，解题的关键是灵活运用所学知识解决问题，正确寻找全等三角形解决问题，属于中考常考题型．