题目内容
8.在平面直角坐标系xOy中,对于点P(x,y),我们把点P1(-y+1,x+1)叫做点P的伴随点,已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,…,这样依次得到点A1,A2,A3,…,An,若点A1的坐标为(3,1),则点A2015的坐标为( )| A. | (0,4) | B. | (-3,1) | C. | (0,-2) | D. | (3,1) |
分析 根据伴随点的定义,罗列出部分点A的坐标,根据点A的变化找出规律“A4n+1(3,1),A4n+2(0,4),A4n+3(-3,1),A4n+4(0,-2)(n为自然数)”,根据此规律即可解决问题.
解答 解:观察,发现规律:A1(3,1),A2(0,4),A3(-3,1),A4(0,-2),A5(3,1),…,
∴A4n+1(3,1),A4n+2(0,4),A4n+3(-3,1),A4n+4(0,-2)(n为自然数).
∵2015=4×503+3,
∴点A2015的坐标为(-3,1).
故选B.
点评 本题考查了规律型中的点的坐标,解题的关键是发现规律“A4n+1(3,1),A4n+2(0,4),A4n+3(-3,1),A4n+4(0,-2)(n为自然数)”.本题属于基础题,难度不大,解决该题型题目时,罗列出部分点的坐标,根据点的坐标的变化发现规律是关键.

练习册系列答案
相关题目
16.已知点P1(x1,y1)和点P2(x2,y2)是正比例函数y=-x+1图象上的两点,则下列判断正确的是( )
| A. | y1>y2 | B. | y1<y2 | C. | 当x1<x2时,y1>y2 | D. | 当x1<x2时,y1<y2 |
3.若整数x能使分式$\frac{3x-3}{{x}^{2}-1}$的值是整数,则符合条件的x的值有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
20. 如图,直线y=$\frac{1}{2}$x+2交x轴于A点,将一块等腰直角三角形纸板的直角顶点置于原点O,另两个顶点M、N恰好落在直线y=$\frac{1}{2}$x+2上.则S△M0N=( )
如图,直线y=$\frac{1}{2}$x+2交x轴于A点,将一块等腰直角三角形纸板的直角顶点置于原点O,另两个顶点M、N恰好落在直线y=$\frac{1}{2}$x+2上.则S△M0N=( )
 如图,直线y=$\frac{1}{2}$x+2交x轴于A点,将一块等腰直角三角形纸板的直角顶点置于原点O,另两个顶点M、N恰好落在直线y=$\frac{1}{2}$x+2上.则S△M0N=( )
如图,直线y=$\frac{1}{2}$x+2交x轴于A点,将一块等腰直角三角形纸板的直角顶点置于原点O,另两个顶点M、N恰好落在直线y=$\frac{1}{2}$x+2上.则S△M0N=( )| A. | $\frac{12}{5}$ | B. | $\frac{14}{5}$ | C. | $\frac{16}{5}$ | D. | 4 |
 一艘船在小岛A的南偏西37°方向的B处,AB=20海里,船自西向东航行1.5小时后到达C处,测得小岛A在点C的北偏西50°方向,求该船航行的速度(精确到0.1海里/小时?)
一艘船在小岛A的南偏西37°方向的B处,AB=20海里,船自西向东航行1.5小时后到达C处,测得小岛A在点C的北偏西50°方向,求该船航行的速度(精确到0.1海里/小时?) 如图,△ABC内接于⊙O,∠B=30°,AC=2cm,求⊙O的半径.
如图,△ABC内接于⊙O,∠B=30°,AC=2cm,求⊙O的半径. 如图,若△ABC的边AB=2,AC=3,Ⅰ、Ⅱ、Ⅲ分别表示以AB、BC、AC为边的正方形,则图中三个阴影部分面积之和为3$\sqrt{5}$.
如图,若△ABC的边AB=2,AC=3,Ⅰ、Ⅱ、Ⅲ分别表示以AB、BC、AC为边的正方形,则图中三个阴影部分面积之和为3$\sqrt{5}$.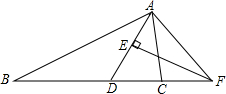 如图,在△ABC中,AD平分∠BAC,EF垂直平分AD交BC的延长线于点F,判断∠CAF与∠B的大小关系,并说明理由.
如图,在△ABC中,AD平分∠BAC,EF垂直平分AD交BC的延长线于点F,判断∠CAF与∠B的大小关系,并说明理由.