题目内容
17. 如图,若△ABC的边AB=2,AC=3,Ⅰ、Ⅱ、Ⅲ分别表示以AB、BC、AC为边的正方形,则图中三个阴影部分面积之和为3$\sqrt{5}$.
如图,若△ABC的边AB=2,AC=3,Ⅰ、Ⅱ、Ⅲ分别表示以AB、BC、AC为边的正方形,则图中三个阴影部分面积之和为3$\sqrt{5}$.
分析 把△CFH绕点C顺时针旋转90°,使CF与BC重合,H旋转到H'的位置,根据旋转的性质和正方形的性质有A、C、H'在一直线上,且BC为△ABH'的中线,得到S△CHF=S△BCH′=S△ABC,同理:S△BGI=S△ADE=S△ABC,根据三角形的面积公式,可得答案.
解答 解:如图,把△CFH绕点C顺时针旋转90°,使CF与BC重合,H旋转到H'的位置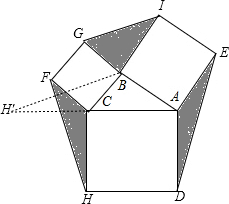
∵四边形ACHD为正方形,∠ACH=90°,CA=CH=CH′,
∴A、C、H'在一直线上,且BC为△ABH'的中线,
∴S△CHF=S△BCH′=S△ABC,
同理:S△ADE=S△BGI=S△ABC,
所以阴影部分面积之和为S△ABC的3倍,
又∵AB=2,AC=3,
∴BC=$\sqrt{A{C}^{2}-A{B}^{2}}=\sqrt{{3}^{2}-{2}^{2}}=\sqrt{5}$
∴S阴影部分面积=3S△ABC=3×$\frac{1}{2}×$AB×BC=3×$\frac{1}{2}$×$\sqrt{5}$×2=3$\sqrt{5}$.
故答案为:3$\sqrt{5}$.
点评 本题考查了勾股定理,利用了旋转的性质:旋转前后图形全等得出S△CHF=S△BCH′,再利用三角形中线分三角形的面积相等得出S△BCH′=S△ABC是解题关键.

练习册系列答案
 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
 △ABC中,AB=AC,DE垂直平分AB(如图),∠A=25°,则∠EBC=52.5°.
△ABC中,AB=AC,DE垂直平分AB(如图),∠A=25°,则∠EBC=52.5°.



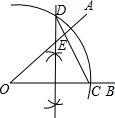 如图,∠AOB=40°,在射线OB上取点C,以O为圆心,OC长为半径作圆弧,交OC的垂直平分线于点D(点D在OC上方),连结CD交OA于点E,则∠AEC=100度.
如图,∠AOB=40°,在射线OB上取点C,以O为圆心,OC长为半径作圆弧,交OC的垂直平分线于点D(点D在OC上方),连结CD交OA于点E,则∠AEC=100度.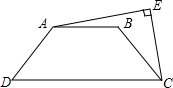 如图,在等腰梯形ABCD中,AB∥CD,AB=6,CD=14,∠AEC=90°,CE=CB,则AE2=84.
如图,在等腰梯形ABCD中,AB∥CD,AB=6,CD=14,∠AEC=90°,CE=CB,则AE2=84.