题目内容
13. 如图,△ABC内接于⊙O,∠B=30°,AC=2cm,求⊙O的半径.
如图,△ABC内接于⊙O,∠B=30°,AC=2cm,求⊙O的半径.
分析 连接OA、OC,根据圆周角定理得到∠AOC=60°,证明△AOC是等边三角形,半径即可求得.
解答 解:连接OA、OC,如图所示: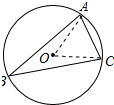
∵∠B=30°,
∴∠AOC=60°,
∵OA=OC,
∴△AOC是等边三角形,
∴OA=AC=2.
点评 本题考查了圆周角定理、等边三角形的判定与性质;熟练运用圆周角定理,证明△OAC是等边三角形是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.在平面直角坐标系xOy中,对于点P(x,y),我们把点P1(-y+1,x+1)叫做点P的伴随点,已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,…,这样依次得到点A1,A2,A3,…,An,若点A1的坐标为(3,1),则点A2015的坐标为( )
| A. | (0,4) | B. | (-3,1) | C. | (0,-2) | D. | (3,1) |
18.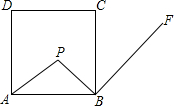 如图,点P是边长为5的正方形ABCD内一点,且PB=2,PB⊥BF,垂足为点B,请在射线BF上找一点M,使得以B,M,C为顶点的三角形与△ABP相似,则BM等于( )
如图,点P是边长为5的正方形ABCD内一点,且PB=2,PB⊥BF,垂足为点B,请在射线BF上找一点M,使得以B,M,C为顶点的三角形与△ABP相似,则BM等于( )
 如图,点P是边长为5的正方形ABCD内一点,且PB=2,PB⊥BF,垂足为点B,请在射线BF上找一点M,使得以B,M,C为顶点的三角形与△ABP相似,则BM等于( )
如图,点P是边长为5的正方形ABCD内一点,且PB=2,PB⊥BF,垂足为点B,请在射线BF上找一点M,使得以B,M,C为顶点的三角形与△ABP相似,则BM等于( )| A. | 2或$\frac{25}{2}$ | B. | 2 | C. | $\frac{25}{2}$ | D. | 2或$\frac{15}{2}$ |
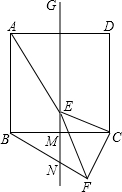 已知如图,正方形ABCD中,GM是其对称轴,E点是线段GM上的点,连接CE,以CE为直角边作等腰直角三角形CEF,∠ECF=90°,连接FB交直线GM于N
已知如图,正方形ABCD中,GM是其对称轴,E点是线段GM上的点,连接CE,以CE为直角边作等腰直角三角形CEF,∠ECF=90°,连接FB交直线GM于N 如图,△ABC中,AB=AC=16cm,AB的垂直平分线ED交AC于D点.
如图,△ABC中,AB=AC=16cm,AB的垂直平分线ED交AC于D点. △ABC中,AB=AC,DE垂直平分AB(如图),∠A=25°,则∠EBC=52.5°.
△ABC中,AB=AC,DE垂直平分AB(如图),∠A=25°,则∠EBC=52.5°.