题目内容
8.一个四边形满足:它的每个顶点到其他三个顶点的距离之和相等,试证明该四边形为矩形.分析 根据每一个顶点到其他三个顶点距离之和都相等,可得S=AB+AD+AC…①,S=BA+BD+BC…②,S=CA+CB+CD…③,S=DA+DB+DC…④,然后由②相等④得(1),由①相等③得(2),再由(1)+(2)可得AD=BC,再证明DC=AB,即可判定四边形的形状是平行四边形,再根据
解答 证明:
以A点的角度看,S=AB+AD+AC…①,
以B点的角度看,S=BA+BD+BC…②,
以C点的角度看,S=CA+CB+CD…③,
以D点的角度看,S=DA+DB+DC…④,
由②、④得AD+DC=AB+BC…(1),
由①、③得BA+AD=CB+CD…(2),
由(1)+(2)得,
2AD=2BC,所以AD=BC,
把这个结论代入(1)得DC=AB,
所以四边形ABCD是平行四边形,
同理可得AC=BD,
所以四边形ABCD是矩形.
点评 此题主要考查矩形的判定,解答此题的关键是利用每一个顶点到其他三个顶点距离之和都相等,列出各个等式,然后得出CD=AB,AD=BC,AC=BD.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知?ABCD中,对角线AC、BD相交于点O,∠ABD=2∠CBD,AE⊥BD.求证:AB=2EO.
已知?ABCD中,对角线AC、BD相交于点O,∠ABD=2∠CBD,AE⊥BD.求证:AB=2EO. 如图所示,已知△ABC中,AB=AC,∠BAD=30°,AD=AE,求∠EDC的度数.
如图所示,已知△ABC中,AB=AC,∠BAD=30°,AD=AE,求∠EDC的度数. 图中的两个三角形有几对相等的角?这两个三角形全等吗?请说明理由.
图中的两个三角形有几对相等的角?这两个三角形全等吗?请说明理由.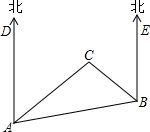 如图,C岛在A岛的北偏东55°方向,B岛在A岛的北偏东85°方向,C岛在B岛的北偏西40°方向,从C岛看A、B两岛的视角∠ACB是多少度?
如图,C岛在A岛的北偏东55°方向,B岛在A岛的北偏东85°方向,C岛在B岛的北偏西40°方向,从C岛看A、B两岛的视角∠ACB是多少度? 如图,在矩形ABCD中,AB=6cm,BC=10cm,点P从点A出发,沿AB边向点B以1cm/s的速度移动,同时点Q从点B出发沿BC边向点C以2cm/s的速度移动,如果P,Q两点同时出发,当一个点到达终点时,另一个点立即停止移动,点P运动时间为t秒.
如图,在矩形ABCD中,AB=6cm,BC=10cm,点P从点A出发,沿AB边向点B以1cm/s的速度移动,同时点Q从点B出发沿BC边向点C以2cm/s的速度移动,如果P,Q两点同时出发,当一个点到达终点时,另一个点立即停止移动,点P运动时间为t秒.