题目内容
18. 已知?ABCD中,对角线AC、BD相交于点O,∠ABD=2∠CBD,AE⊥BD.求证:AB=2EO.
已知?ABCD中,对角线AC、BD相交于点O,∠ABD=2∠CBD,AE⊥BD.求证:AB=2EO.
分析 取AB的中点F,连接EF、OF,根据直角三角形斜边上的中线等于斜边的一半可得EF=BF=$\frac{1}{2}$AB,根据等边对等角可得∠ABD=∠BEF,根据三角形的中位线平行于第三边并且等于第三边的一半可得OF∥BC,根据两直线平行,内错角相等可得∠DBC=∠EOF,然后根据三角形的一个外角等于与它不相邻的两个内角的和求出∠EFO=∠EOF,再根据等角对等边可得EF=OE,从而得证.
解答 证明:如图,取AB的中点F,连接EF、OF,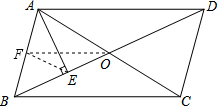 ∵AE⊥BD,
∵AE⊥BD,
∴EF=BF=$\frac{1}{2}$AB,
∴∠ABD=∠BEF,
∵AO=CO,
∴OF是△ABC的中位线,
∴OF∥BC,
∴∠DBC=∠EOF,
根据三角形的外角性质,∠BEF=∠EFO+∠EOF,
又∵∠ABD=2∠DBC,
∴∠EFO=∠EOF,
∴EF=OE,
∴OE=$\frac{1}{2}$AB,
∴AB=2OE.
点评 本题考查了平行四边形的对边平行,对角线互相平分的性质,直角三角形斜边上的中线等于斜边的一半,三角形的中位线平行于第三边并且等于第三边的一半,三角形的一个外角等于与它不相邻的两个内角的和的性质,作辅助线是解题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
8.在直角坐标系内,下列结论成立的是( )
| A. | 点(4,3)与点(3,4)表示同一个点 | |
| B. | 平面内的任一点到两坐标轴的距离相等 | |
| C. | 若点P(x,y)的坐标满足xy=0,则点P在坐标轴上 | |
| D. | 点P(m,n)到x轴的距离为m,到y轴的距离为n |
7.下列方程是三元一次方程的是( )
| A. | x+3y=$\frac{1}{7}$z+3 | B. | xy+z=8 | C. | y+3z=7 | D. | xy+xz=11 |