题目内容
10.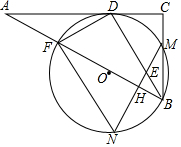 如图,在Rt△ABC中,∠C=90°,BD为∠ABC的平分线,DF⊥BD交AB于点F,△BDF的外接圆⊙O与边BC相交于点M,过点M作AB的垂线交BD于点E,交⊙O于点N,交AB于点H,连接FN.
如图,在Rt△ABC中,∠C=90°,BD为∠ABC的平分线,DF⊥BD交AB于点F,△BDF的外接圆⊙O与边BC相交于点M,过点M作AB的垂线交BD于点E,交⊙O于点N,交AB于点H,连接FN.(1)求证:AC是⊙O的切线;
(2)若AF=1,tan∠N=$\frac{4}{3}$,求⊙O的半径r的长;
(3)在(2)的条件下,求BE的长.
分析 (1)根据题意结合角平分线的定义得出∠OBD=∠DBC,进而求出∠ODB+∠BDC=90°,进而得出答案;
(2)构造直角三角形,设OD=3k,AD=4k,则AO=5k,则AO=OD+AF=3k+1,进而得出答案;
(3)利用相似三角形的判定与性质和三角函数关系分别得出BH,BC,BD的长,进而求出BE的长.
解答 (1)证明:连接OD,
∵OD=OB,
∴∠ODB=∠OBD,
∵BD平分∠ABC,
∴∠OBD=∠DBC,
∵∠DBC+∠CDB=90°,
∴∠ODB+∠BDC=90°,
∴OD⊥AC,
∴AC为⊙O的切线;
(2)解:∵∠FNH=∠ABC,OD⊥AC,BC⊥AC,
∴OD∥BC,
∴∠AOD=∠ABC=∠FNH,
在Rt△AOD中,设OD=3k,AD=4k,则AO=5k,
∵AO=OD+AF=3k+1,
∴3k+1=5k,
解得:k=$\frac{1}{2}$,
∴r=3k=$\frac{3}{2}$;
(3)解:连接BN,
由题意可得:BF=2r=3,
∵∠FNH+∠BNH=∠BNH+∠NBH=90°,
∴∠FNH=∠NBH,
∴$\frac{NH}{BH}$=$\frac{4}{3}$,
∵$\frac{FH}{HN}$=$\frac{4}{3}$,
∴设BH=3a,则HN=4a,故FH=$\frac{16}{3}$a,
则$\frac{16}{3}$a+3a=3,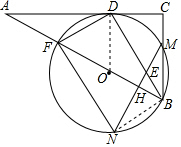
解得:a=$\frac{9}{25}$,
故BH=$\frac{27}{25}$,
∵DO∥BC,
∴△ADO∽△ACB,
∴$\frac{DO}{BC}$=$\frac{AO}{AB}$,
∴$\frac{\frac{3}{2}}{BC}$=$\frac{1+\frac{3}{2}}{4}$,
解得:BC=$\frac{12}{5}$,
∵∠C=∠FDB=90°,∠ABD=∠CBD,
∴△BCD∽△BDF,
则$\frac{BD}{BF}$=$\frac{BC}{BD}$,
故BD2=BF•BC=$\frac{36}{5}$,
∴BD=$\frac{6}{5}$$\sqrt{5}$,
∵∠EHB=∠BCD=90°,∠ABD=∠CBD,
∴△BHE∽△BCD,
则$\frac{BE}{BD}$=$\frac{BH}{BC}$,
∴BE=$\frac{BH}{BC}$•BD=$\frac{27}{50}$$\sqrt{5}$.
点评 此题主要考查了圆的综合以及相似三角形的判定与性质、三角函数关系等知识,正确得出△BHE∽△BCD是解题关键.

| A. | a≠1 | B. | a>1 | C. | a≥2 | D. | -1<a≤2 |
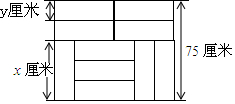 如图,10块相同的长方形墙砖拼成一个矩形,设长方形墙砖的长和宽分别为x厘米和y厘米,则依题意列方程组正确的是( )
如图,10块相同的长方形墙砖拼成一个矩形,设长方形墙砖的长和宽分别为x厘米和y厘米,则依题意列方程组正确的是( )| A. | $\left\{\begin{array}{l}{x+2y=75}\\{y=3x}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{2x+y=75}\\{x=3y}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{2x+y=75}\\{y=3x}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+2y=75}\\{x=3y}\end{array}\right.$ |
| A. | 0.6579×103 | B. | 6.579×102 | C. | 6.579×106 | D. | 65.79×105 |
 如图,下列条件中不能判定AB∥CD的是( )
如图,下列条件中不能判定AB∥CD的是( )| A. | ∠1=∠5 | B. | ∠1+∠4=180° | C. | ∠2=∠4 | D. | ∠3=∠4 |
| A. | 1.796×106 | B. | 17.96×106 | C. | 1.796×107 | D. | 0.1796×107 |

| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
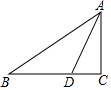 如图,△ACB中,∠ACB=Rt∠,已知∠B=α,∠ADC=β,AB=a,则BD的长可表示为( )
如图,△ACB中,∠ACB=Rt∠,已知∠B=α,∠ADC=β,AB=a,则BD的长可表示为( )| A. | a•(cosα-cosβ) | B. | $\frac{a}{tanβ-tanα}$ | ||
| C. | acosα-$\frac{a•sinα}{tanβ}$ | D. | a•cosα-asinα•a•tanβ |