题目内容
20.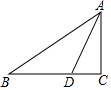 如图,△ACB中,∠ACB=Rt∠,已知∠B=α,∠ADC=β,AB=a,则BD的长可表示为( )
如图,△ACB中,∠ACB=Rt∠,已知∠B=α,∠ADC=β,AB=a,则BD的长可表示为( )| A. | a•(cosα-cosβ) | B. | $\frac{a}{tanβ-tanα}$ | ||
| C. | acosα-$\frac{a•sinα}{tanβ}$ | D. | a•cosα-asinα•a•tanβ |
分析 利用锐角三角函数关系分别表示出BC,DC的长进而得出答案.
解答 解:∵∠C=90°,∠B=α,∠ADC=β,AB=a,
∴cosB=cosα=$\frac{BC}{AB}$=$\frac{BC}{a}$,
则BC=a•cosα,
sinB=sinα=$\frac{AC}{AB}$=$\frac{AC}{a}$,
故AC=a•sinα,
则tanβ=$\frac{AC}{DC}$,
故DC=$\frac{AC}{tanβ}$=$\frac{a•sinα}{tanβ}$,
则BD=BC-DC=a•cosα-$\frac{a•sinα}{tanβ}$.
故选:C.
点评 此题主要考查了锐角三角函数的定义,正确表示出DC的长是解题关键.

练习册系列答案
相关题目
11.圆的半径为r厘米,若半径增加3厘米,则新圆的面积比原来圆的面积增加了( )
| A. | 9π平方厘米 | B. | 3π(2r-3)平方厘米 | C. | 3π(2r+3)平方厘米 | D. | π(r+3)2平面厘米 |
15.若点P是第三象限内的点,且点P到x轴的距离是4,到y轴的距离是3,则点P的坐标是( )
| A. | (-4,-3) | B. | (4,-3) | C. | (-3,-4) | D. | (3,-4) |
5.地球绕太阳每小时转动通过的路程约是1.1×105千米,用科学记数法表示地球一天(以24小时计)转动通过的路程约是( )
| A. | 0.264×107千米 | B. | 2.64×106千米 | C. | 26.4×105千米 | D. | 264×104千米 |
5.用-a表示的数一定是( )
| A. | 负数 | B. | 正数或负数 | C. | 负整数 | D. | 以上全不对 |
2. 如图,在△ABC中,AB=6cm,∠B=∠C=30°,那么△ABC的中线AD=( )cm.
如图,在△ABC中,AB=6cm,∠B=∠C=30°,那么△ABC的中线AD=( )cm.
 如图,在△ABC中,AB=6cm,∠B=∠C=30°,那么△ABC的中线AD=( )cm.
如图,在△ABC中,AB=6cm,∠B=∠C=30°,那么△ABC的中线AD=( )cm.| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
3. 下列图中,哪个可以通过如图图形平移得到( )
下列图中,哪个可以通过如图图形平移得到( )
 下列图中,哪个可以通过如图图形平移得到( )
下列图中,哪个可以通过如图图形平移得到( )| A. |  | B. |  | C. |  | D. |  |
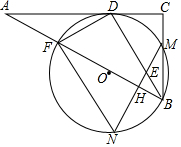 如图,在Rt△ABC中,∠C=90°,BD为∠ABC的平分线,DF⊥BD交AB于点F,△BDF的外接圆⊙O与边BC相交于点M,过点M作AB的垂线交BD于点E,交⊙O于点N,交AB于点H,连接FN.
如图,在Rt△ABC中,∠C=90°,BD为∠ABC的平分线,DF⊥BD交AB于点F,△BDF的外接圆⊙O与边BC相交于点M,过点M作AB的垂线交BD于点E,交⊙O于点N,交AB于点H,连接FN.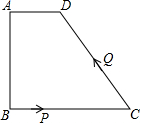 如图,四边形ABCD中,AD∥BC,∠A=90°,AD=1cm,AB=3cm,BC=5cm,动点P从点B出发以1cm/s的速度沿BC的方向运动,动点Q从点C出发以2cm/s的速度沿CD方向运动,P、Q两点同时出发,当Q到达点D时停止运动,点P也随之停止,设运动的时间为ts(t>0)
如图,四边形ABCD中,AD∥BC,∠A=90°,AD=1cm,AB=3cm,BC=5cm,动点P从点B出发以1cm/s的速度沿BC的方向运动,动点Q从点C出发以2cm/s的速度沿CD方向运动,P、Q两点同时出发,当Q到达点D时停止运动,点P也随之停止,设运动的时间为ts(t>0)