题目内容
20.数的概念是从实践中产生和发展起来的,在学习了实数以后,像x2=-1这样的方程还是没有实数解的,因为没有一个实数的平方等于-1,即负数在实数范围内没有平方根,所以为了了解形如x2=-1这类方程的解,就要引入一个新的数i.定义:如果一个数的平方等于-1,记为i2=-1,这个数i叫做虚数单位.在这种情况下,i可以与实数b相乘再同实数a相加从而得到形如“a+bi”(a、b为实数)的数,人们把这种数叫作复数,a叫这个复数的实部,b叫做这个复数的虚部.它的加、减、乘法运算与整式的加、减、乘法运算类似.比如:(2+i)+(5-3i)=(2+5)+(1-3)i=7-2i.请你根据对以上内容的理解,计算:(3+i)(3-i)=10.分析 利用平方差公式进行计算,并将i2=-1代入即可.
解答 解:(3+i)(3-i)=9-i2=9-(-1)=10;
故答案为:10.
点评 本题考查了新定义--复数,明确其加、减、乘法运算与整式的加、减、乘法运算类似即可.

练习册系列答案
相关题目
10.计算机是将信息转换成二进制数进行处理的,二进制即“逢2进1”,如(1101)2表示二进制数,将它转换成十进制形式是1×23+1×22+0×21+1×20=13,那么将二进制(1111)2转换成十进制形式是( )
| A. | 8 | B. | 15 | C. | 30 | D. | 31 |
11.点M(2,-3)到x轴的距离是( )
| A. | 2 | B. | -3 | C. | 3 | D. | 以上都不对 |
8.一次函数y=$\frac{4}{3}$x-b沿y轴平移3个单位得直线与y=$\frac{4}{3}$x-1,则b的值为( )
| A. | -2或4 | B. | 2或-4 | C. | 4或-6 | D. | -4或6 |
5.(1)填空
31-30=3(0 )×2
32-31=3(1 )×2
33-32=3(2 )×2
(2)探索(1)中式子的规律,试写出第n个等式,并说明第n个等式成立.
(3)计算:3+32+…+32017.
31-30=3(0 )×2
32-31=3(1 )×2
33-32=3(2 )×2
(2)探索(1)中式子的规律,试写出第n个等式,并说明第n个等式成立.
(3)计算:3+32+…+32017.
9.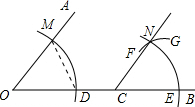 已知,点C在∠AOB的OB边上,用尺规过点C作CN∥OA,作图痕迹如图所示,下列对弧FG的描述,正确的是( )
已知,点C在∠AOB的OB边上,用尺规过点C作CN∥OA,作图痕迹如图所示,下列对弧FG的描述,正确的是( )
 已知,点C在∠AOB的OB边上,用尺规过点C作CN∥OA,作图痕迹如图所示,下列对弧FG的描述,正确的是( )
已知,点C在∠AOB的OB边上,用尺规过点C作CN∥OA,作图痕迹如图所示,下列对弧FG的描述,正确的是( )| A. | 以点C为圆心,OD的长为半径的弧 | B. | 以点C为圆心,OM的长为半径的弧 | ||
| C. | 以点E为圆心,DM的长为半径的弧 | D. | 以点E为圆心,CE的长为半径的弧 |
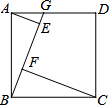 如图,G为正方形ABCD的边AD上的一个动点,AE⊥BG,CF⊥BG,垂足分别为点E,F.已知AD=4,则AE2+CF2=16.
如图,G为正方形ABCD的边AD上的一个动点,AE⊥BG,CF⊥BG,垂足分别为点E,F.已知AD=4,则AE2+CF2=16. 如图,在长方形ABCD中,放入六个形状大小相同的长方形,所标尺寸如图所示,请你利用方程组的思想方法求出图中阴影部分面积是多少cm2?
如图,在长方形ABCD中,放入六个形状大小相同的长方形,所标尺寸如图所示,请你利用方程组的思想方法求出图中阴影部分面积是多少cm2?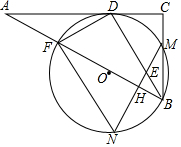 如图,在Rt△ABC中,∠C=90°,BD为∠ABC的平分线,DF⊥BD交AB于点F,△BDF的外接圆⊙O与边BC相交于点M,过点M作AB的垂线交BD于点E,交⊙O于点N,交AB于点H,连接FN.
如图,在Rt△ABC中,∠C=90°,BD为∠ABC的平分线,DF⊥BD交AB于点F,△BDF的外接圆⊙O与边BC相交于点M,过点M作AB的垂线交BD于点E,交⊙O于点N,交AB于点H,连接FN.