题目内容
13.分解因式:$-\frac{1}{2}{x^4}+8$=-$\frac{1}{2}$(x2+4)(x+2)(x-2);(a2+1)2-4a2=(a+1)2(a-1)2.分析 原式提取公因式,再利用平方差公式分解即可;原式利用平方差公式及完全平方公式分解即可.
解答 解:原式=-$\frac{1}{2}$(x4-16)=-$\frac{1}{2}$(x2+4)(x+2)(x-2);原式=(a2+1+2a)(a2+1-2a)=(a+1)2(a-1)2,
故答案为:-$\frac{1}{2}$(x2+4)(x+2)(x-2);(a+1)2(a-1)2
点评 此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
1.运用等式性质的变形,正确的是( )
| A. | 如果a=b,那么a+c=b-c | B. | 如果$\frac{a}{c}=\frac{b}{c}$,那么a=b | ||
| C. | 如果a=b,那么$\frac{a}{c}=\frac{b}{c}$ | D. | 如果a=3,那么a2=3a2 |
2.下列计算正确的是( )
| A. | ($\frac{1}{2}$)0=$\frac{1}{2}$ | B. | (-2)-1=$\frac{1}{2}$ | C. | -2×(-5)=10 | D. | 2-3=1 |
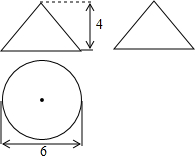 已知某几何体的三视图如图所示(单位:cm),则它的侧面展开图的面积是15πcm2.
已知某几何体的三视图如图所示(单位:cm),则它的侧面展开图的面积是15πcm2.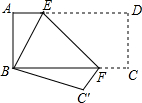 如图,将长方形纸片ABCD折叠,使点D与点B重合,点C落在点C'处,折痕为EF.如果∠ABE=20°,那么∠EFB=55度.
如图,将长方形纸片ABCD折叠,使点D与点B重合,点C落在点C'处,折痕为EF.如果∠ABE=20°,那么∠EFB=55度.