题目内容
1.运用等式性质的变形,正确的是( )| A. | 如果a=b,那么a+c=b-c | B. | 如果$\frac{a}{c}=\frac{b}{c}$,那么a=b | ||
| C. | 如果a=b,那么$\frac{a}{c}=\frac{b}{c}$ | D. | 如果a=3,那么a2=3a2 |
分析 利用等式的性质对每个等式进行变形即可找出答案.
解答 解:A、利用等式性质1,两边都加c,得到a+c=b+c,所以A不成立;
B、利用等式性质2,两边都乘以c,得到a=b,所以B成立;
C、不成立,因为c必需不为0;
D、因为a2=9,3a2=27,所以a2≠3a2;
故选B.
点评 主要考查了等式的基本性质.
等式性质:1、等式的两边同时加上或减去同一个数或字母,等式仍成立;
2、等式的两边同时乘以或除以同一个不为0数或字母,等式仍成立.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
12.已知∠BAC=90°,半径为r的圆O与两条直角边AB,AC都相切,设AB=a(a>r),BE与圆O相切于点E.现给出下列命题:①当∠ABE=60°时,BE=$\sqrt{3}r$; ②当∠ABE=90°时,BE=r;则下列判断正确的是( )
| A. | 命题①是真命题,命题②是假命题 | B. | 命题①②都是真命题 | ||
| C. | 命题①是假命题,命题②是真命题 | D. | 命题①②都是假命题 |
16.下列:①${({-\frac{1}{5}})^{-2}}=25$;②(-2016)0=1;③(a-b)2=a2-b2;④(-2ab3)3=-8a3b9;⑤5x2-6x=-x.其中计算正确的是( )
| A. | ①②③ | B. | ①②④ | C. | ③④⑤ | D. | ②④⑤ |
6.设方程x2-5x+k=0的一个根比另一个根的2倍少1,则k的值为( )
| A. | $\frac{44}{9}$ | B. | 6 | C. | -6 | D. | 15 |
11.某市努力改善空气质量,近年来空气质量明显好转,根据该市环境保护局公布的2010-2014这五年各年全年空气质量优良的天数如表所示,根据表中信息回答:
(1)这五年的全年空气质量优良天数的中位数是245,平均数是243;
(2)这五年的全年空气质量优良天数与它前一年相比增加最多的是2012年(填写年份);
(3)求这五年的全年空气质量优良天数的方差.
| 2010 | 2011 | 2012 | 2013 | 2014 |
| 234 | 233 | 245 | 247 | 256 |
(2)这五年的全年空气质量优良天数与它前一年相比增加最多的是2012年(填写年份);
(3)求这五年的全年空气质量优良天数的方差.
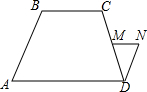 如图,在梯形ABCD中,AD∥BC,M是CD中点,MN∥AD,DN∥AB,设BC=a,AD=b(a<b),那么MN与a、b有怎样的数量关系.试加以证明.
如图,在梯形ABCD中,AD∥BC,M是CD中点,MN∥AD,DN∥AB,设BC=a,AD=b(a<b),那么MN与a、b有怎样的数量关系.试加以证明. 如图,在Rt△ABC中,∠ACB=90°,BD是∠ABC的平分线,点O在AC上,⊙O经过B,D两点,交BC于点E.
如图,在Rt△ABC中,∠ACB=90°,BD是∠ABC的平分线,点O在AC上,⊙O经过B,D两点,交BC于点E.