题目内容
4.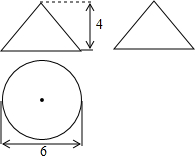 已知某几何体的三视图如图所示(单位:cm),则它的侧面展开图的面积是15πcm2.
已知某几何体的三视图如图所示(单位:cm),则它的侧面展开图的面积是15πcm2.
分析 首先根据几何体的三视图判断该几何体为圆锥,然后根据尺寸求得侧面积即可.
解答 解:观察三视图发现该几何体为圆锥,其底面半径为6,高为4,
故圆锥的母线长为$\sqrt{{3}^{2}+{4}^{2}}$=5,
所以圆锥的侧面积为πrl=π×3×5=15πcm2,
故答案为:15π.
点评 本题考查了圆锥的计算及由三视图判断几何题的知识,解题的关键是能够确定该几何体的形状并熟知圆锥的侧面积的计算公式,难度不大.

练习册系列答案
相关题目
12.已知∠BAC=90°,半径为r的圆O与两条直角边AB,AC都相切,设AB=a(a>r),BE与圆O相切于点E.现给出下列命题:①当∠ABE=60°时,BE=$\sqrt{3}r$; ②当∠ABE=90°时,BE=r;则下列判断正确的是( )
| A. | 命题①是真命题,命题②是假命题 | B. | 命题①②都是真命题 | ||
| C. | 命题①是假命题,命题②是真命题 | D. | 命题①②都是假命题 |
19.若线段CD是由线段AB平移得到的,点A(-1,3)的对应点为C(2,2),则点B(-3,-1)的对应点D的坐标是( )
| A. | (0,-2) | B. | (1,-2) | C. | (-2,0) | D. | (4,6) |

 如图,在Rt△ABC中,∠ACB=90°,BD是∠ABC的平分线,点O在AC上,⊙O经过B,D两点,交BC于点E.
如图,在Rt△ABC中,∠ACB=90°,BD是∠ABC的平分线,点O在AC上,⊙O经过B,D两点,交BC于点E.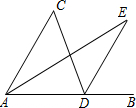 如图,点B是AD延长线上的一点,DE∥AC,AE平分∠CAB,∠C=50°,∠E=30°,则∠CDA的度数等于70°.
如图,点B是AD延长线上的一点,DE∥AC,AE平分∠CAB,∠C=50°,∠E=30°,则∠CDA的度数等于70°.