题目内容
5．写出以$4+\sqrt{17}、4-\sqrt{17}$为两根的关于x的一元二次方程x2-8x-1=0．分析 根据根与系数的关系：两根之和=-$\frac{b}{a}$，两根之积=$\frac{c}{a}$，首先写出两根之和，再写出两根之积，可直接得到方程．
解答 解：∵4+$\sqrt{17}$+4-$\sqrt{17}$=8，（4+$\sqrt{17}$）×（4-$\sqrt{17}$）=-1，
∴方程为：x2-8x-1=0．
故答案为：x2-8x-1=0．
点评 本题考查了一元二次方程ax2+bx+c=0（a≠0）根与系数的关系：若方程的两根分别为x1，x2，则x1+x2=-$\frac{b}{a}$，x1•x2=$\frac{c}{a}$．
练习册系列答案
名校课堂系列答案
相关题目
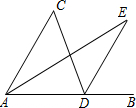如图，点B是AD延长线上的一点，DE∥AC，AE平分∠CAB，∠C=50°，∠E=30°，则∠CDA的度数等于70°．
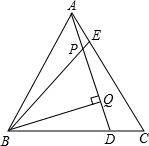如图，在等边△ABC中，点D、E分别在边BC、AC上，且AE=CD，BE与AD相交于点P，BQ⊥AD于点Q．