题目内容
 如图,请根据图象所提供的信息解答下列问题:
如图,请根据图象所提供的信息解答下列问题:(1)交点P的坐标(1,1)是一元二次方程组:
(2)不等式kx+b<0的解集是
(3)当x
(4)若直线l1分别交x轴、y轴于点M、A,直线l2分别交x轴、y轴于点B、N,求点M的坐标和四边形OMPN的面积.
考点:一次函数与二元一次方程(组),一次函数与一元一次不等式
专题:计算题
分析:(1)利用函数图象交点坐标为两函数解析式组成的方程组的解进行解答;
(2)观察函数图象,写出直线y=kx+b在x轴下方所对应的自变量的范围即可;
(3)根据函数图象,当x≤1时,直线y=kx+b没有在直线y=mx+n的下方,即kx+b≥mx+n;
(4)先利用待定系数法确定直线l1和l2的解析式,再根据坐标轴上点的坐标特征确定M点和N点坐标,然后利用四边形OMPN的面积=S△ONB-S△PMB进行计算.
(2)观察函数图象,写出直线y=kx+b在x轴下方所对应的自变量的范围即可;
(3)根据函数图象,当x≤1时,直线y=kx+b没有在直线y=mx+n的下方,即kx+b≥mx+n;
(4)先利用待定系数法确定直线l1和l2的解析式,再根据坐标轴上点的坐标特征确定M点和N点坐标,然后利用四边形OMPN的面积=S△ONB-S△PMB进行计算.
解答:解:(1)交点P的坐标(1,1)是一元二次方程组
的解;
(2)不等式kx+b<0的解集为x>3;
(3)当x≤1时,kx+b≥mx+n;
(4)把A(0,-1),P(1,1)分别代入y=mx+n得
,解得
,
所以直线l1的解析式为y=2x-1,
当y=0时,2x-1=0,解得x=
,
所以M点的坐标为(
,0);
把P(1,1)、B(3,0)分别代入y=kx+b得
,解得
,
所以直线l2的解析式为y=-
x+
,
当x=0时,y=-
x+
=
,则N点坐标为(0,
),
所以四边形OMPN的面积=S△ONB-S△PMB
=
×3×
-
×(3-
)×1
=1.
故答案为
;x>3;≤1.
|
(2)不等式kx+b<0的解集为x>3;
(3)当x≤1时,kx+b≥mx+n;
(4)把A(0,-1),P(1,1)分别代入y=mx+n得
|
|
所以直线l1的解析式为y=2x-1,
当y=0时,2x-1=0,解得x=
| 1 |
| 2 |
所以M点的坐标为(
| 1 |
| 2 |
把P(1,1)、B(3,0)分别代入y=kx+b得
|
|
所以直线l2的解析式为y=-
| 1 |
| 2 |
| 3 |
| 2 |
当x=0时,y=-
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
所以四边形OMPN的面积=S△ONB-S△PMB
=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=1.
故答案为
|
点评:本题考查了一次函数与二元一次方程组、与一元一次不等式的关系,函数图象交点坐标为两函数解析式组成的方程组的解.也考查了待定系数法求一次函数解析式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某班抽取6名同学参加体能测试,成绩如下:80,90,75,75,80,80.下列表述错误的是( )
| A、平均数是80 |
| B、极差是15 |
| C、中位数是80 |
| D、标准差是25 |
 如图,Rt△AOB的边OA长为2,边AB长为1,OA在数轴上,以O为圆心,以OB为半径画弧,交数轴的正半轴于点C,则点C表示的实数是( )
如图,Rt△AOB的边OA长为2,边AB长为1,OA在数轴上,以O为圆心,以OB为半径画弧,交数轴的正半轴于点C,则点C表示的实数是( )| A、2.236 | ||
B、
| ||
| C、2.5 | ||
D、
|

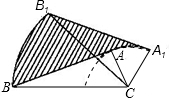 如图,在Rt△ABC中,∠BAC=90°,AB=6cm,AC=3cm,将△ABC绕顶点C按顺时针方向旋转45°至△A1B1C1的位置,则线段AB扫过区域(图中的阴影部分)的面积为
如图,在Rt△ABC中,∠BAC=90°,AB=6cm,AC=3cm,将△ABC绕顶点C按顺时针方向旋转45°至△A1B1C1的位置,则线段AB扫过区域(图中的阴影部分)的面积为 如图,直线y=2x-2与双曲线y=
如图,直线y=2x-2与双曲线y=