题目内容
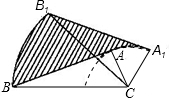 如图,在Rt△ABC中,∠BAC=90°,AB=6cm,AC=3cm,将△ABC绕顶点C按顺时针方向旋转45°至△A1B1C1的位置,则线段AB扫过区域(图中的阴影部分)的面积为
如图,在Rt△ABC中,∠BAC=90°,AB=6cm,AC=3cm,将△ABC绕顶点C按顺时针方向旋转45°至△A1B1C1的位置,则线段AB扫过区域(图中的阴影部分)的面积为考点:扇形面积的计算,旋转的性质
专题:
分析:根据阴影部分的面积是:S扇形BCB1+S△CB1A1-S△ABC-S扇形CAA1,分别求得:扇形BCB1的面积,S△CB1A1,S△ABC以及扇形CAA1的面积,即可求解.
解答:解:在Rt△ABC中,BC=
=
=3
,
扇形BCB1的面积是=
=
,
S△CB1A1=
×6×3=9;
S扇形CAA1=
=
.
故S阴影部分=S扇形BCB1+S△CB1A1-S△ABC-S扇形CAA1=
+9-9-
=
(cm2).
故答案是:
cm2.
| AC2+AB2 |
| 62+32 |
| 5 |
扇形BCB1的面积是=
45π(3
| ||
| 360 |
| 45π |
| 8 |
S△CB1A1=
| 1 |
| 2 |
S扇形CAA1=
| 45π×32 |
| 360 |
| 9π |
| 8 |
故S阴影部分=S扇形BCB1+S△CB1A1-S△ABC-S扇形CAA1=
| 45π |
| 8 |
| 9π |
| 8 |
| 9π |
| 2 |
故答案是:
| 9π |
| 2 |
点评:本题考查了扇形面积的计算,理解阴影部分的面积等于S扇形BCB1+S△CB1A1-S△ABC-S扇形CAA1是关键.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
方程x2-x-1=
的解的情况是( )
| 1 |
| x-1 |
| A、仅有一正根 |
| B、仅有一负根 |
| C、一正根一负根 |
| D、两个不相等的实数根 |
石家庄市10月份某七天的最低气温(单位:℃)分别为14,10,11,14,14,13,8,则这组数据中的中位数和众数分别是( )
| A、13,13 |
| B、14,14 |
| C、13,14 |
| D、14,13 |
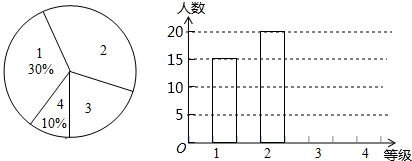 新的交通法规实施后,驾校的考试规则也发生了变化,考试共设四个科目:科目1、科目2、科目3和科目4,以下简记为:1、2、3、4.四个科目考试在同一地点进行,但每个学员每次只能够参加一个科目考试.在某次考试中,对该考点各科目考试人数进行了调查统计,并根据调查结果绘制成如图所示的条形统计图和扇形统计图(未完成),请结合图中所给信息解答下列问题:
新的交通法规实施后,驾校的考试规则也发生了变化,考试共设四个科目:科目1、科目2、科目3和科目4,以下简记为:1、2、3、4.四个科目考试在同一地点进行,但每个学员每次只能够参加一个科目考试.在某次考试中,对该考点各科目考试人数进行了调查统计,并根据调查结果绘制成如图所示的条形统计图和扇形统计图(未完成),请结合图中所给信息解答下列问题: 如图,请根据图象所提供的信息解答下列问题:
如图,请根据图象所提供的信息解答下列问题: