题目内容
某超市在“元旦”促销期间规定:超市内所有商品按标价的75%出售,同时当顾客在消费满一定金额后,按如下方案获得相应金额的奖券:
根据上述促销方法知道,顾客在超市内购物可以获得双重优惠,即顾客在超市内购物获得的优惠额=商品的折扣+相应的奖券金额,例如:购买标价为440元的商品,则消费金额为:440×75%=330元,获得的优惠额为:440×(l-75%)+40=150元.
(1)购买一件标价为800元的商品,求获得的优惠额;
(2)若购买一件商品的消费金额在450≤a<800之间,请用含a的代数式表示优惠额;
(3)对于标价在600元与900元之间(含600元和900元)的商品,顾客购买标价为多少元的商品时可以得到
的优惠率?(设购买该商品得到的优惠率=购买商品获得的优惠额÷商品的标价)
| 消费金额a(元)的范围 | 100≤a<400 | 400≤a<600 | 600≤a<800 |
| 获得奖券金额(元) | 40 | 100 | 130 |
(1)购买一件标价为800元的商品,求获得的优惠额;
(2)若购买一件商品的消费金额在450≤a<800之间,请用含a的代数式表示优惠额;
(3)对于标价在600元与900元之间(含600元和900元)的商品,顾客购买标价为多少元的商品时可以得到
| 13 |
| 32 |
考点:一元一次方程的应用
专题:
分析:(1)先求出标价为450元的商品按80%的价格出售,消费金额为360元,再根据消费金额360元在200≤x≤400之间,即可得出优惠额;
(2)分两种情况:当400<a≤600时;当600≤a<800时;讨论可求该顾客获得的优惠额;
(3)设购买标价为x元时,可以得到
的优惠率,根据(2)的计算方法列出方程解答即可.
(2)分两种情况:当400<a≤600时;当600≤a<800时;讨论可求该顾客获得的优惠额;
(3)设购买标价为x元时,可以得到
| 13 |
| 32 |
解答:解:(1)优惠额为800×(l-75%)+130=330元;
(2)消费金额在400<a≤600之间时,优惠额为a(1-75%)+100=0.25a+100;
消费金额在600≤a<800之间时,优惠额为a(1-75%)+130=0.25a+130;
(3)设购买标价为x元时,由题意得
0.25x+130=
x,
解得:x=832.
答:购买标价为832元的商品时可以得到
的优惠率.
(2)消费金额在400<a≤600之间时,优惠额为a(1-75%)+100=0.25a+100;
消费金额在600≤a<800之间时,优惠额为a(1-75%)+130=0.25a+130;
(3)设购买标价为x元时,由题意得
0.25x+130=
| 13 |
| 32 |
解得:x=832.
答:购买标价为832元的商品时可以得到
| 13 |
| 32 |
点评:此题考查一元一次方程的实际运用,列代数式,理解题意,找出运算的方法是解决问题的关键.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
嘉绍跨海大桥在2013年7月19日建成通车,此项目总投资约139亿元,139亿元用科学记数法表示为( )
| A、1.39×1010元 |
| B、1.39×1011元 |
| C、0.139×1012元 |
| D、13.9×109元 |
方程x2-x-1=
的解的情况是( )
| 1 |
| x-1 |
| A、仅有一正根 |
| B、仅有一负根 |
| C、一正根一负根 |
| D、两个不相等的实数根 |
 如图,摆放有五杂梅花,下列说法错误的是(以中心梅花为初始位置)( )
如图,摆放有五杂梅花,下列说法错误的是(以中心梅花为初始位置)( )| A、左上角的梅花只需沿对角线平移即可 |
| B、右上角的梅花需先沿对角线平移后,再顺时针旋转45° |
| C、右下角的梅花需先沿对角线平移后,再顺时针旋转180 |
| D、左下角的梅花需先沿对角线平移后,再顺时针旋转90° |
 已知:如图,AB∥DE,AC∥DF,BE=CF,AB=3cm.求DE的长.
已知:如图,AB∥DE,AC∥DF,BE=CF,AB=3cm.求DE的长.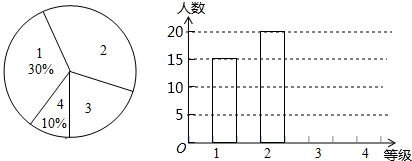 新的交通法规实施后,驾校的考试规则也发生了变化,考试共设四个科目:科目1、科目2、科目3和科目4,以下简记为:1、2、3、4.四个科目考试在同一地点进行,但每个学员每次只能够参加一个科目考试.在某次考试中,对该考点各科目考试人数进行了调查统计,并根据调查结果绘制成如图所示的条形统计图和扇形统计图(未完成),请结合图中所给信息解答下列问题:
新的交通法规实施后,驾校的考试规则也发生了变化,考试共设四个科目:科目1、科目2、科目3和科目4,以下简记为:1、2、3、4.四个科目考试在同一地点进行,但每个学员每次只能够参加一个科目考试.在某次考试中,对该考点各科目考试人数进行了调查统计,并根据调查结果绘制成如图所示的条形统计图和扇形统计图(未完成),请结合图中所给信息解答下列问题: 如图,请根据图象所提供的信息解答下列问题:
如图,请根据图象所提供的信息解答下列问题: