题目内容
3.某等腰三角形的顶角是80°,则一腰上的高与底边所成的角的度数( )| A. | 40° | B. | 60° | C. | 80° | D. | 100° |
分析 结合题意画出图形,可先求得两底角的大小,在再结合直角三角形两锐角互余可求得答案.
解答  解:如图,在△ABC中,AB=AC,∠BAC=80°,过C作CD⊥AB,垂足为D,
解:如图,在△ABC中,AB=AC,∠BAC=80°,过C作CD⊥AB,垂足为D,
∴∠B=$\frac{180°-∠A}{2}$=50°,
∵CD⊥AB,
∴∠B+∠DCB=90°,
∴∠DCB=90°-50°=40°,
即一腰上的高与底边所成的角为40°,
故选A.
点评 本题主要考查等腰三角形的性质,掌握等腰三角形两底角相等和三角形内角和定理是解题的关键.

练习册系列答案
相关题目
8.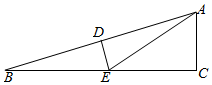 如图所示,在△ABC中,∠ACB=90°,∠B=15°,DE垂直平分AB,交BC于点E,BE=6cm,则AC等于( )
如图所示,在△ABC中,∠ACB=90°,∠B=15°,DE垂直平分AB,交BC于点E,BE=6cm,则AC等于( )
 如图所示,在△ABC中,∠ACB=90°,∠B=15°,DE垂直平分AB,交BC于点E,BE=6cm,则AC等于( )
如图所示,在△ABC中,∠ACB=90°,∠B=15°,DE垂直平分AB,交BC于点E,BE=6cm,则AC等于( )| A. | 6cm | B. | 5cm | C. | 4cm | D. | 3cm |
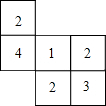 一个几何体由大小相同的小立方块搭成,从上面观察这个几何体看到的形状如图所示,其中小正方形里的数字表示该位置小立方块的个数,请画出从正面、左面看到的这个几何体的形状图.
一个几何体由大小相同的小立方块搭成,从上面观察这个几何体看到的形状如图所示,其中小正方形里的数字表示该位置小立方块的个数,请画出从正面、左面看到的这个几何体的形状图. 有理数a、b、c在数轴上的位置如图所示,化简|a+b|+|a|+|b|.
有理数a、b、c在数轴上的位置如图所示,化简|a+b|+|a|+|b|. 如图,△ABC中,∠A=80°,BE,CF交于点O,∠ACF=30°,∠ABE=20°,求∠BOC的度数.
如图,△ABC中,∠A=80°,BE,CF交于点O,∠ACF=30°,∠ABE=20°,求∠BOC的度数. 有理数a,b,c在数轴上如图所示,试化简|2c-b|+|a+b|-|2a-c|.
有理数a,b,c在数轴上如图所示,试化简|2c-b|+|a+b|-|2a-c|.