题目内容
18.解方程:y-$\frac{{y}^{2}-1}{2}$=-$\frac{1}{3}$.分析 先去分母,整理后求出b2-4ac的值,再代入公式求出即可.
解答 解 y-$\frac{{y}^{2}-1}{2}$=-$\frac{1}{3}$,
去分母,得6y-3(y2-1)=-2,
整理,得3y2-6y-5=0,
b2-4ac=(-6)2-4×3×(-5)=96,
y=$\frac{6±\sqrt{96}}{2×3}$,
y1=$\frac{3+2\sqrt{6}}{3}$,y2=$\frac{3-2\sqrt{6}}{3}$.
点评 本题考查了解一元二次方程的应用,能选择适当的方法解一元二次方程是解此题的关键.

练习册系列答案
相关题目
8.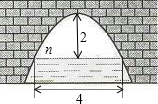 如图是抛物线形拱桥,当拱顶高离水面2m时,水面宽4m.水面下降2.5m,水面宽度增加( )
如图是抛物线形拱桥,当拱顶高离水面2m时,水面宽4m.水面下降2.5m,水面宽度增加( )
 如图是抛物线形拱桥,当拱顶高离水面2m时,水面宽4m.水面下降2.5m,水面宽度增加( )
如图是抛物线形拱桥,当拱顶高离水面2m时,水面宽4m.水面下降2.5m,水面宽度增加( )| A. | 1m | B. | 2m | C. | 3m | D. | 6m |
9.当x-y=-3时,代数式-4-x+y的值等于( )
| A. | -1 | B. | 7 | C. | -7 | D. | 1 |
6.$\sqrt{m-n}$的一个有理化因式是( )
| A. | $\sqrt{m+n}$ | B. | $\sqrt{m-n}$ | C. | $\sqrt{m}$+$\sqrt{n}$ | D. | $\sqrt{m}$-$\sqrt{n}$ |
3.某等腰三角形的顶角是80°,则一腰上的高与底边所成的角的度数( )
| A. | 40° | B. | 60° | C. | 80° | D. | 100° |
 如图,已知l1∥l2,∠A=40°,∠1=60°,则∠2的度数为80°.
如图,已知l1∥l2,∠A=40°,∠1=60°,则∠2的度数为80°.