题目内容
16.若a,b都是正整数,且a<b,$\sqrt{a}$与$\sqrt{b}$是可以合并二次根式,是否存在a,b,使$\sqrt{a}$+$\sqrt{b}$=$\sqrt{75}$?若存在,请求出a,b的值;若不存在,请说明理由.分析 直接利用同类二次根式的定义得出$\sqrt{a}$,$\sqrt{b}$与$\sqrt{3}$是同类二次根式,进而得出答案.
解答 解:∵$\sqrt{a}$与$\sqrt{b}$是可以合并二次根式,$\sqrt{a}$+$\sqrt{b}$=$\sqrt{75}$,
∴$\sqrt{a}$+$\sqrt{b}$=$\sqrt{75}$=5$\sqrt{3}$,
∴当a=3,则b=48,
当a=12,则b=27.
点评 此题主要考查了同类二次根式,正确得出$\sqrt{a}$,$\sqrt{b}$与$\sqrt{3}$是同类二次根式是解题关键.

练习册系列答案
相关题目
7. 如图,CD为△ABC的中线,且CD⊥AC,O为BC边上一点,以O为圆心,0C为长半径作⊙O,若⊙O与AB恰好相切于点D,则tanB=( )
如图,CD为△ABC的中线,且CD⊥AC,O为BC边上一点,以O为圆心,0C为长半径作⊙O,若⊙O与AB恰好相切于点D,则tanB=( )
 如图,CD为△ABC的中线,且CD⊥AC,O为BC边上一点,以O为圆心,0C为长半径作⊙O,若⊙O与AB恰好相切于点D,则tanB=( )
如图,CD为△ABC的中线,且CD⊥AC,O为BC边上一点,以O为圆心,0C为长半径作⊙O,若⊙O与AB恰好相切于点D,则tanB=( )| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | $\frac{3}{8}$ | D. | $\frac{1}{2}$ |
8.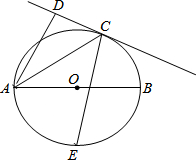 如图,AB是⊙O的直径,直线CD与⊙O相切于点C,AD⊥CD,垂足为D,E是弧AB的中点,若AD=$\frac{32}{5}$,AC=8,则CE的长为( )
如图,AB是⊙O的直径,直线CD与⊙O相切于点C,AD⊥CD,垂足为D,E是弧AB的中点,若AD=$\frac{32}{5}$,AC=8,则CE的长为( )
 如图,AB是⊙O的直径,直线CD与⊙O相切于点C,AD⊥CD,垂足为D,E是弧AB的中点,若AD=$\frac{32}{5}$,AC=8,则CE的长为( )
如图,AB是⊙O的直径,直线CD与⊙O相切于点C,AD⊥CD,垂足为D,E是弧AB的中点,若AD=$\frac{32}{5}$,AC=8,则CE的长为( )| A. | 7$\sqrt{2}$ | B. | 7$\sqrt{3}$ | C. | 8$\sqrt{2}$ | D. | 3+4$\sqrt{2}$ |
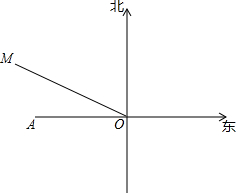 如图,根据天气预报,台风中心位于A市正东方向300km的点O处,正以20km/h的速度向北偏西60°方向移动,距离台风中心250km范围内都会受到影响,若台风移动的速度和方向不变,则A市受台风影响的时间是有多长?
如图,根据天气预报,台风中心位于A市正东方向300km的点O处,正以20km/h的速度向北偏西60°方向移动,距离台风中心250km范围内都会受到影响,若台风移动的速度和方向不变,则A市受台风影响的时间是有多长?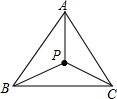 如图,点P是正△ABC内一点.
如图,点P是正△ABC内一点.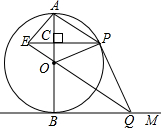 如图,AB是⊙0的直径,BM切⊙0于点B,点P是⊙0上的一个动点(不经过A、B两点),过点0作OQ∥AP交BM于点Q,过点P作PE⊥AB于点C,交QO的延长线于点E,连接PQ.
如图,AB是⊙0的直径,BM切⊙0于点B,点P是⊙0上的一个动点(不经过A、B两点),过点0作OQ∥AP交BM于点Q,过点P作PE⊥AB于点C,交QO的延长线于点E,连接PQ.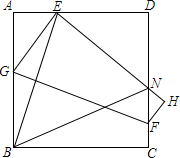 如图,四边形ABCD是正方形,E是AD边上一点,将正方形折叠,使点B与点E重合,FG是折痕,C点落在H上,EH与CD交于点N.求证:∠EBN=45°.
如图,四边形ABCD是正方形,E是AD边上一点,将正方形折叠,使点B与点E重合,FG是折痕,C点落在H上,EH与CD交于点N.求证:∠EBN=45°.