题目内容
4.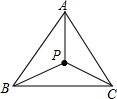 如图,点P是正△ABC内一点.
如图,点P是正△ABC内一点.(1)以点B为旋转中心,将△PBC逆时针旋转60°,试画出旋转后的图形;
(2)若PB=3,PC=4,∠BPC=150°,请求出PA的长.
分析 (1)根据中心旋转的定义作出图形即可.
(2)先证明△BEP是等边三角形,再证明△AEP是直角三角形,利用勾股定理即可解决.
解答 解:(1)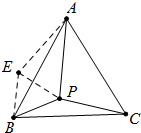 以点B为旋转中心,将△PBC逆时针旋转60°,△BAE就是所求的三角形.
以点B为旋转中心,将△PBC逆时针旋转60°,△BAE就是所求的三角形.
(2)∵△ABC是等边三角形,
∴∠ABC=60°,
∵△BAE是由△BCP逆时针旋转60°得到,
∴BP=BE=3,AE=PC=4,∠EBP=60°,∠BPC=∠BEA=150°
∴△EBP是等边三角形,
∴EP=PB=EB=3,∠BEP=60°,
∴∠AEP=∠AEB-∠BEP=90°,
在RT△AEP中,∵∠AEP=90°,AE=4,EP=3,
∴AP=$\sqrt{A{E}^{2}+E{P}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5.
点评 本题考查旋转变换、等边三角形的判定和性质、勾股定理等知识,解题的关键是通过旋转添加辅助线构造特殊三角形,利用特殊三角形解决问题,属于中考常考题型.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
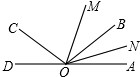 如图,已知O为AD上一点,∠AOC与∠AOB互补,OM,ON分别为∠AOC,∠AOB的平分线,若∠MON=50°,试求∠AOC与∠AOB的度数.
如图,已知O为AD上一点,∠AOC与∠AOB互补,OM,ON分别为∠AOC,∠AOB的平分线,若∠MON=50°,试求∠AOC与∠AOB的度数.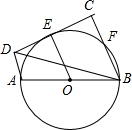 如图,AB是⊙O的直径,CD切⊙O于E,AD⊥CD于点D,BC⊥CD于交⊙O于F,且BF=CF,若AB=6.求BD的长.
如图,AB是⊙O的直径,CD切⊙O于E,AD⊥CD于点D,BC⊥CD于交⊙O于F,且BF=CF,若AB=6.求BD的长.