题目内容
8.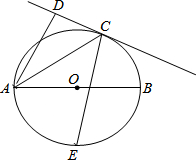 如图,AB是⊙O的直径,直线CD与⊙O相切于点C,AD⊥CD,垂足为D,E是弧AB的中点,若AD=$\frac{32}{5}$,AC=8,则CE的长为( )
如图,AB是⊙O的直径,直线CD与⊙O相切于点C,AD⊥CD,垂足为D,E是弧AB的中点,若AD=$\frac{32}{5}$,AC=8,则CE的长为( )| A. | 7$\sqrt{2}$ | B. | 7$\sqrt{3}$ | C. | 8$\sqrt{2}$ | D. | 3+4$\sqrt{2}$ |
分析 首先连接OC,由直线CD与⊙O相切于点C,AD⊥CD,易证得OC∥AD,继而可得AC平分∠DAB,然后连接BC,OE,过点A作AF⊥CE于点F,可证得△ADC∽△ACB,△ACB∽△AFE,△ACF是等腰直角三角形,然后由相似三角形的对应边成比例以及勾股定理,即可求得答案.
解答 解:连接BC,OE,OC,过点A作AF⊥EC于点F,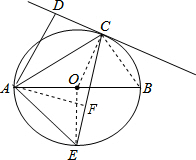 ∵直线CD与⊙O相切于点C,
∵直线CD与⊙O相切于点C,
∴OC⊥CD,
∵AD⊥CD,
∴OC∥AD,
∴∠DAC=∠OCA,
∵OA=OC,
∴∠OCA=∠OAC,
∴∠OAC=∠DAC,
即AC平分∠DAB;
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ACB=∠ADC,
∵∠DAC=∠BAC,
∴△ADC∽△ACB,
∴$\frac{AD}{AC}=\frac{AC}{AB}$,
即$\frac{\frac{32}{5}}{8}=\frac{8}{AB}$,
解得:AB=10,
∴BC=$\sqrt{{AB}^{2}{-AC}^{2}}$=6,
∵点E为$\widehat{AB}$的中点,
∴∠AOE=90°,
∴OE=OA=$\frac{1}{2}$AB=5,
∴AE=$\sqrt{{OA}^{2}{+OE}^{2}}$=5$\sqrt{2}$,
∵∠AEF=∠B(同弧所对圆周角相等),∠AFE=∠ACB=90°,
∴△ACB∽△AFE,
∴$\frac{AB}{AE}=\frac{AC}{AF}$,
∴$\frac{10}{5\sqrt{2}}=\frac{8}{AF}$,
∴AF=4$\sqrt{2}$,EF=3$\sqrt{2}$,
∵∠ACF=$\frac{1}{2}$∠AOE=45°,
∴△ACF是等腰直角三角形,
∴CF=AF=4$\sqrt{2}$,
∴CE=CF+EF=7$\sqrt{2}$.
故选A.
点评 此题考查了切线的性质、相似三角形的判定与性质、勾股定理以及等腰直角三角形性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案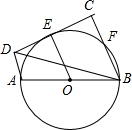 如图,AB是⊙O的直径,CD切⊙O于E,AD⊥CD于点D,BC⊥CD于交⊙O于F,且BF=CF,若AB=6.求BD的长.
如图,AB是⊙O的直径,CD切⊙O于E,AD⊥CD于点D,BC⊥CD于交⊙O于F,且BF=CF,若AB=6.求BD的长.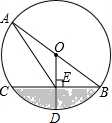 如图,已知AB是⊙O的直径,半径OD⊥BC于点E,连结AE,$\widehat{CD}$=60°.
如图,已知AB是⊙O的直径,半径OD⊥BC于点E,连结AE,$\widehat{CD}$=60°.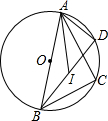 如图,△ABC内接于⊙O,AB为⊙O的直径,点I是△ABC的内心,延长BI交⊙O于D,若AC=4,BC=3,求BI•ID的值.
如图,△ABC内接于⊙O,AB为⊙O的直径,点I是△ABC的内心,延长BI交⊙O于D,若AC=4,BC=3,求BI•ID的值.