题目内容
11.已如⊙O与⊙O′内切于A点,⊙O与⊙O′的半径分别为R和r(R>r),P为⊙O上一点,PT切⊙O′于T点,连结AP交⊙O′于B点.求证:PA2:PT2=R:(R-r).分析 作出辅助线,根据圆的特点,判断出OP∥O′B,得到比例式,结合切割线定理即可.
解答 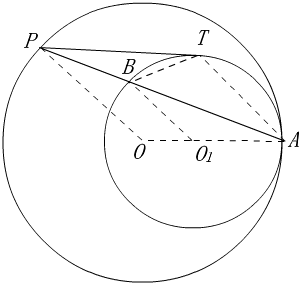
证明:如图,连接AT,BT,BO1,PO,
∵OA=OP,O1A=O1B,
∴∠OPA=∠OAP=∠O1BA,
∴OP∥O1B,
∴$\frac{PA}{PB}$=$\frac{OA}{A{O}_{1}}$=$\frac{R}{R-r}$,
由切割线定理得,PT2=PA×PB,
∴$\frac{P{A}^{2}}{P{T}^{2}}$=$\frac{P{A}^{2}}{PA×PB}$=$\frac{PA}{PB}$=$\frac{R}{R-r}$,
∴PA2:PT2=R:(R-r).
点评 此题是相切两圆的性质,主要考查了切割线定理,和圆中两半径围成的三角形的特点,作出辅助线是解决本题的关键,也是难点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,抛物线y=ax2+bx+c与y轴正半轴相交,其顶点坐标为(-$\frac{1}{2}$,1),有下列结论:①ac<0;②a-b=1;③4ac<b2;④a-b+c<0,其中正确结论的个数是( )
如图,抛物线y=ax2+bx+c与y轴正半轴相交,其顶点坐标为(-$\frac{1}{2}$,1),有下列结论:①ac<0;②a-b=1;③4ac<b2;④a-b+c<0,其中正确结论的个数是( )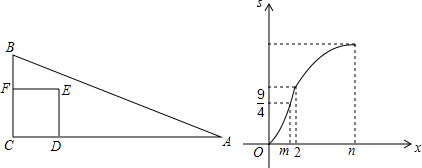
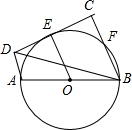 如图,AB是⊙O的直径,CD切⊙O于E,AD⊥CD于点D,BC⊥CD于交⊙O于F,且BF=CF,若AB=6.求BD的长.
如图,AB是⊙O的直径,CD切⊙O于E,AD⊥CD于点D,BC⊥CD于交⊙O于F,且BF=CF,若AB=6.求BD的长. 如图,△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于F.
如图,△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于F.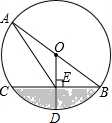 如图,已知AB是⊙O的直径,半径OD⊥BC于点E,连结AE,$\widehat{CD}$=60°.
如图,已知AB是⊙O的直径,半径OD⊥BC于点E,连结AE,$\widehat{CD}$=60°.