题目内容
19. 如图,将矩形ABCD沿线段AE翻折,使点B恰好落在边AD上的点F处,再沿边EF将矩形ABCD剪开,所得的另一个矩形ECDF和原来的矩形相似,则原来的矩形ABCD的宽AB与长AD的比值为$\frac{\sqrt{5}-1}{2}$.
如图,将矩形ABCD沿线段AE翻折,使点B恰好落在边AD上的点F处,再沿边EF将矩形ABCD剪开,所得的另一个矩形ECDF和原来的矩形相似,则原来的矩形ABCD的宽AB与长AD的比值为$\frac{\sqrt{5}-1}{2}$.
分析 根据翻折变换的性质得到AB=AF,根据相似多边形的性质得到比例式,整理得到一元二次方程,解方程即可.
解答 解:由翻折变换的性质可知,AB=AF,
则FD=AD-AF=AD-AB,
∵矩形ECDF和矩形ABCD相似,
∴$\frac{DF}{AB}$=$\frac{AB}{AD}$,即AB2=(AD-AB)•AD,
整理得,($\frac{AB}{AD}$)2+$\frac{AB}{AD}$-1=0,
解得,$\frac{AB}{AD}$=$\frac{\sqrt{5}-1}{2}$,
故答案为:$\frac{\sqrt{5}-1}{2}$.
点评 本题考查的是相似多边形的性质,掌握相似多边形的性质:对应角相等;对应边的比相等是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,BC∥ED,计算AB、AC的长.(使用证明的方法)
如图,BC∥ED,计算AB、AC的长.(使用证明的方法) 观察函数y=2x-5的图象,回答下列问题:
观察函数y=2x-5的图象,回答下列问题: 如图,矩形草坪长30m、宽20m,沿草坪四周有1m宽的环形小路,小路内外边缘形成的两个矩形相似吗?说出你的理由.
如图,矩形草坪长30m、宽20m,沿草坪四周有1m宽的环形小路,小路内外边缘形成的两个矩形相似吗?说出你的理由.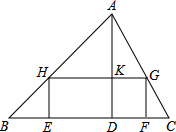 如图,在△ABC中,AD⊥BC于点D,矩形EFGH的四个顶点在三角形的三边上,已知BC=9cm,AD=8cm,EF=5cm,求矩形EFGH的面积.
如图,在△ABC中,AD⊥BC于点D,矩形EFGH的四个顶点在三角形的三边上,已知BC=9cm,AD=8cm,EF=5cm,求矩形EFGH的面积.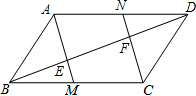 如图,在平行四边形ABCD中,M、N分别为BC、DA中点,AM、CN分别交BD于点E、F,求证:BE=EF=FD.
如图,在平行四边形ABCD中,M、N分别为BC、DA中点,AM、CN分别交BD于点E、F,求证:BE=EF=FD.