题目内容
10. 观察函数y=2x-5的图象,回答下列问题:
观察函数y=2x-5的图象,回答下列问题:(1)x取哪些值时,2x-5=0?
(2)x取哪些值时,2x-5>0?
(3)x取哪些值时,2x-5<0?
(4)x取哪些值时,2x-5>3?
分析 (1)图象与x轴交点的横坐标的值即为方程2x-5=0的解;
(2)一次函数y=2x-5的图象在x轴上方的部分对应的x的取值,即为2x-5>0的解集;
(3)一次函数y=2x-5的图象在x轴下方的部分对应的x的取值,即为2x-5<0的解集;
(4)由图象可知,当y=3时,x=4,一次函数y=2x-5的图象在x=4的右边对应的x的取值,即为2x-5>3的解集.
解答 解:(1)由图象可知,当x=$\frac{5}{2}$时,2x-5=0;
(2)由图象可知,当x>$\frac{5}{2}$时,2x-5>0;
(3)由图象可知,当x<$\frac{5}{2}$时,2x-5<0;
(4)由图象可知,当x>4时,2x-5>3.
点评 此题主要考查了一次函数与一元一次不等式的关系:从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.也考查了一次函数与一元一次方程,利用数形结合是解题的关键.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
20.某种细胞每过30分便由1个分裂成2个,经过3时,这种细胞由一个分裂成( )
| A. | 6个 | B. | 8个 | C. | 64个 | D. | 12个 |
 在Rt△ABC中,∠C=90°,D为BC边(除端点外)上的一点,设∠ADC=α,∠B=β,
在Rt△ABC中,∠C=90°,D为BC边(除端点外)上的一点,设∠ADC=α,∠B=β,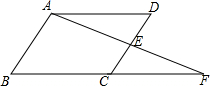 如图,在?ABCD中,CE=$\frac{1}{2}$ED,AE,BC的延长线交于点F.若△ECF的面积为1.求四边形ABCE的面积.
如图,在?ABCD中,CE=$\frac{1}{2}$ED,AE,BC的延长线交于点F.若△ECF的面积为1.求四边形ABCE的面积. 如图,将矩形ABCD沿线段AE翻折,使点B恰好落在边AD上的点F处,再沿边EF将矩形ABCD剪开,所得的另一个矩形ECDF和原来的矩形相似,则原来的矩形ABCD的宽AB与长AD的比值为$\frac{\sqrt{5}-1}{2}$.
如图,将矩形ABCD沿线段AE翻折,使点B恰好落在边AD上的点F处,再沿边EF将矩形ABCD剪开,所得的另一个矩形ECDF和原来的矩形相似,则原来的矩形ABCD的宽AB与长AD的比值为$\frac{\sqrt{5}-1}{2}$.