题目内容
10.已知点P是∠ABC内一动点(P与B点不重合),连接BP,过P作PE⊥BA于E,PF⊥BC于F.设∠EBP=α,∠FBP=β,(α、β都是锐角)(1)当∠EBP=40°,∠FBP=20°时,请比较sin40°与sin20°的大小(直接写出结果);
(2)若PE>PF,试比较sinα与sinβ的大小,并说明理由;
(3)若α>β.试判断cosα与cosβ的大小,并给出证明.
分析 (1)根据题意画出图形,可得出PE>PF,从而证出sin40°>sin20°,
(2)根据sin∠EBP=$\frac{PE}{BP}$,sin∠FBP=$\frac{PF}{BP}$,PE>PF,BP=BP,即可得出sinα>sinβ;
(3)先根据cos∠EBP=$\frac{BE}{BP}$=cosα,cos∠FBP=$\frac{BF}{BP}$=cosβ,得出PE>PF,再证出BE<BF,即可得出cosα<cosβ.
解答 解:(1)如图:根据图形可得:PE>PF,
则sin40°>sin20°,
(2)∵sin∠EBP=$\frac{PE}{BP}$,sin∠FBP=$\frac{PF}{BP}$,PE>PF,BP=BP,
∴$\frac{PE}{BP}>\frac{PF}{BP}$,
∴sinα>sinβ;
(3)∵cos∠EBP=$\frac{BE}{BP}$=cosα,cos∠FBP=$\frac{BF}{BP}$=cosβ,
∵BP=BP,α>β,
∴PE>PF,
∵BE=$\sqrt{B{P}^{2}-P{E}^{2}}$,
BF=$\sqrt{B{P}^{2}-P{F}^{2}}$,
∴BE<BF,
∴cosα<cosβ.
点评 此题考查了解直角三角形,用到的知识点是勾股定理、解直角三角形,关键是根据题意画出图形,比较出有关结果的大小.

练习册系列答案
相关题目
 如图,将矩形ABCD沿线段AE翻折,使点B恰好落在边AD上的点F处,再沿边EF将矩形ABCD剪开,所得的另一个矩形ECDF和原来的矩形相似,则原来的矩形ABCD的宽AB与长AD的比值为$\frac{\sqrt{5}-1}{2}$.
如图,将矩形ABCD沿线段AE翻折,使点B恰好落在边AD上的点F处,再沿边EF将矩形ABCD剪开,所得的另一个矩形ECDF和原来的矩形相似,则原来的矩形ABCD的宽AB与长AD的比值为$\frac{\sqrt{5}-1}{2}$. 如图,蚂蚁在距巢穴2米远找到一只苍蝇,决定将其搬回家,可蚂蚁每一分钟内前进1米,却被风刮退2米,请问这只蚂蚁能否回到巢穴?如不能,请说明理由;如能,算一算何时能回巢穴.
如图,蚂蚁在距巢穴2米远找到一只苍蝇,决定将其搬回家,可蚂蚁每一分钟内前进1米,却被风刮退2米,请问这只蚂蚁能否回到巢穴?如不能,请说明理由;如能,算一算何时能回巢穴.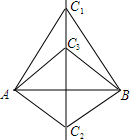 已知:如图,C1A=C1B,C2A=C2B.C3是直线C1C2上一点.求证:C3A=C3B.
已知:如图,C1A=C1B,C2A=C2B.C3是直线C1C2上一点.求证:C3A=C3B.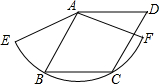 如图,已知菱形ABCD的边长为3 cm,B,C两点在扇形AEF的$\widehat{EF}$上,求$\widehat{BC}$的长度及扇形ABC的面积.
如图,已知菱形ABCD的边长为3 cm,B,C两点在扇形AEF的$\widehat{EF}$上,求$\widehat{BC}$的长度及扇形ABC的面积. 如图,在边长为2cm的正△ABC中,分别以A,B,C点为圆心,1cm长为半径作$\widehat{DE}$、$\widehat{EF}$、$\widehat{FD}$,求阴影部分的面积.
如图,在边长为2cm的正△ABC中,分别以A,B,C点为圆心,1cm长为半径作$\widehat{DE}$、$\widehat{EF}$、$\widehat{FD}$,求阴影部分的面积.