题目内容
11.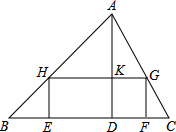 如图,在△ABC中,AD⊥BC于点D,矩形EFGH的四个顶点在三角形的三边上,已知BC=9cm,AD=8cm,EF=5cm,求矩形EFGH的面积.
如图,在△ABC中,AD⊥BC于点D,矩形EFGH的四个顶点在三角形的三边上,已知BC=9cm,AD=8cm,EF=5cm,求矩形EFGH的面积.
分析 根据矩形的性质得到HG∥BC,HG=EF=5cm,根据平行线的性质得到AD⊥HG,通过△AHG∽△ABC,得到$\frac{HG}{BC}=\frac{AK}{AD}$,代入数据即可得到结论.
解答 解:∵四边形HEFG是矩形,
∴HG∥BC,HG=EF=5cm,
∵AD⊥BC于点D,
∴AD⊥HG,
∵GH∥BC,
∴△AHG∽△ABC,
∴$\frac{HG}{BC}=\frac{AK}{AD}$,
即:$\frac{5}{9}=\frac{8-HE}{8}$,
∴HE=$\frac{32}{9}$,
∴矩形EFGH的面积=HE•EF=$\frac{32}{9}$×5=$\frac{160}{9}$.
点评 本题主要考查了矩形的性质和相似三角形的判定与性质,知道相似三角形的对应高之比就等于对应边之比,即相似比.

练习册系列答案
相关题目
 如图,将矩形ABCD沿线段AE翻折,使点B恰好落在边AD上的点F处,再沿边EF将矩形ABCD剪开,所得的另一个矩形ECDF和原来的矩形相似,则原来的矩形ABCD的宽AB与长AD的比值为$\frac{\sqrt{5}-1}{2}$.
如图,将矩形ABCD沿线段AE翻折,使点B恰好落在边AD上的点F处,再沿边EF将矩形ABCD剪开,所得的另一个矩形ECDF和原来的矩形相似,则原来的矩形ABCD的宽AB与长AD的比值为$\frac{\sqrt{5}-1}{2}$. 已知直线a,b,点P是a,b外的任意一点,过点P分别画a,b的垂线.
已知直线a,b,点P是a,b外的任意一点,过点P分别画a,b的垂线.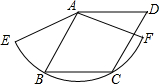 如图,已知菱形ABCD的边长为3 cm,B,C两点在扇形AEF的$\widehat{EF}$上,求$\widehat{BC}$的长度及扇形ABC的面积.
如图,已知菱形ABCD的边长为3 cm,B,C两点在扇形AEF的$\widehat{EF}$上,求$\widehat{BC}$的长度及扇形ABC的面积.