题目内容
10.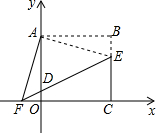 如图,在平面直角坐标系中,正方形OABC的点A在y轴上,点C在x轴上,点B(4,4),点E在BC边上,将△ABE绕点A顺时针旋转90°,得△AOF,连接EF交y轴于点D.
如图,在平面直角坐标系中,正方形OABC的点A在y轴上,点C在x轴上,点B(4,4),点E在BC边上,将△ABE绕点A顺时针旋转90°,得△AOF,连接EF交y轴于点D.(Ⅰ)若点E的坐标为(4,3),求①线段EF的长;②点D的坐标;
(Ⅱ)设点E(4,m),S=S△ABE+S△FCE,试用含m的式子表示S,并求出使S取得最大值时点E的坐标.
分析 (Ⅰ)①由旋转的性质及正方形的性质可知,BE=OF,∠FOC=180°,由B(4,4),E(4,3),可得CE=3,CF=5.然后在Rt△CEF中,利用勾股定理即可求得EF=$\sqrt{C{E}^{2}+C{F}^{2}}$=$\sqrt{34}$;
②由OD∥CE,可得△ODF∽△CEF,根据相似三角形对应边成比例得到$\frac{OD}{CE}$=$\frac{OF}{CF}$,代入数值即可求得OD=$\frac{3}{5}$;
(Ⅱ)由B(4,4),E(4,m),可得BE=4-m,CF=CO+OF=4+4-m=8-m,根据三角形的面积公式求出S△ABE=$\frac{1}{2}$AB•BE=2(4-m),S△FCE=$\frac{1}{2}$CE•CF=$\frac{1}{2}$m(8-m),那么S=2(4-m)+$\frac{1}{2}$m(8-m)=-$\frac{1}{2}$m2+2m+8,利用配方法得到S=-$\frac{1}{2}$(m-2)2+10,根据二次函数的性质即可求出m=2时,S取最大值,此时点E的坐标为(4,2).
解答 解:(Ⅰ)①由题意可知,BE=OF,∠FOC=180°, ∵B(4,4),E(4,3),
∵B(4,4),E(4,3),
∴CE=3,CF=5.
∵在Rt△CEF中,∠ECF=90°,
∴EF=$\sqrt{C{E}^{2}+C{F}^{2}}$=$\sqrt{34}$;
②∵OD∥CE,
∴△ODF∽△CEF,
∴$\frac{OD}{CE}$=$\frac{OF}{CF}$,$\frac{OD}{3}$=$\frac{1}{5}$,
∴OD=$\frac{3}{5}$;
(Ⅱ)∵B(4,4),E(4,m),
∴BE=4-m,CF=CO+OF=4+4-m=8-m,
∴S△ABE=$\frac{1}{2}$AB•BE=2(4-m),S△FCE=$\frac{1}{2}$CE•CF=$\frac{1}{2}$m(8-m),
∴S=2(4-m)+$\frac{1}{2}$m(8-m)=-$\frac{1}{2}$m2+2m+8,
配方,得S=-$\frac{1}{2}$(m-2)2+10,
∴当m=2时,S取最大值,此时点E的坐标为(4,2).
点评 本题是几何变换综合题,其中涉及到旋转的性质,正方形的性质,勾股定理,相似三角形的判定与性质,三角形的面积,二次函数最值的求法等知识,综合性较强,难度适中.利用数形结合是解题的关键.

 53随堂测系列答案
53随堂测系列答案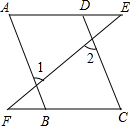 如图,∠1=∠2,∠A=∠C,求证:∠E=∠F.
如图,∠1=∠2,∠A=∠C,求证:∠E=∠F.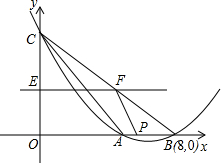 如图,抛物线y=ax2+bx+c(a>0)交x轴于A、B两点,交y轴于C点,A点在B点的左侧,已知B点坐标是(8,0),tan∠ABC=$\frac{1}{2}$,△ABC的面积为8.
如图,抛物线y=ax2+bx+c(a>0)交x轴于A、B两点,交y轴于C点,A点在B点的左侧,已知B点坐标是(8,0),tan∠ABC=$\frac{1}{2}$,△ABC的面积为8.
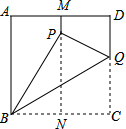 如图,有一张面积为3的正方形纸片ABCD,M,N分别是AD,BC边的中点,将C点折叠至MN上,落在P点的位置,折痕为BQ,连结PQ,则PQ=1.
如图,有一张面积为3的正方形纸片ABCD,M,N分别是AD,BC边的中点,将C点折叠至MN上,落在P点的位置,折痕为BQ,连结PQ,则PQ=1.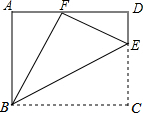 如图,点E是矩形ABCD中CD边上一点,△BCE沿BE折叠为△BFE,点F落在AD上.若sin∠DFE=$\frac{1}{3}$,则 tan∠EBC的值为$\frac{\sqrt{2}}{2}$.
如图,点E是矩形ABCD中CD边上一点,△BCE沿BE折叠为△BFE,点F落在AD上.若sin∠DFE=$\frac{1}{3}$,则 tan∠EBC的值为$\frac{\sqrt{2}}{2}$.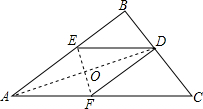 如图,在三角形纸片ABC中,∠BAC为锐角,AB=12cm,AC=15cm.按下列步骤折叠:第一次,把∠B折叠使点B落在AC边上,折痕为AD,交BC于点D;第二次折叠,使点A与点D重合,折痕分别交AB、AC于点E、F,EF与AD交于点O,展开后,连结DE、DF.
如图,在三角形纸片ABC中,∠BAC为锐角,AB=12cm,AC=15cm.按下列步骤折叠:第一次,把∠B折叠使点B落在AC边上,折痕为AD,交BC于点D;第二次折叠,使点A与点D重合,折痕分别交AB、AC于点E、F,EF与AD交于点O,展开后,连结DE、DF.