题目内容
1.一元二次方程x2+px+19=0的两根恰好比方程x2-Ax+B=0的两个根分别大1,其中A,B,p都为整数,则A+B=18.分析 设x2-Ax+B=0两根为α,β,根据根与系数的关系和已知条件得到-p=α+1+β+1,A=α+β,α•β=B,所以将其代入:(α+1)(β+1)=αβ+(α+β)+1=19,得到B+A+1=19.
解答 解:设x2-Ax+B=0两根为α,β,则
-p=α+1+β+1,A=α+β,α•β=B,
所以-p=A+2,
所以(α+1)(β+1)=αβ+(α+β)+1=19,
所以 B+A+1=19,
所以 B+A=18.
故答案是:18.
点评 主要考查一元二次方程根与系数关系的应用.利用根与系数的关系得到两根之间的关系是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.已知方程x2+mx+n=0的两根为x1、x2(x1<x2),方程x2+mx+n-1=0的两根为x3、x4(x3<x4),则下列关系一定成立的是( )
| A. | x1<x2<x3<x4 | B. | x1<x3<x4<x2 | C. | x3<x4<x1<x2 | D. | x3<x1<x2<x4 |
 如图,?ABCD中,AE⊥BC于E,AF⊥CD于F,∠BAD=135°,则∠EAF=45°.
如图,?ABCD中,AE⊥BC于E,AF⊥CD于F,∠BAD=135°,则∠EAF=45°.
 如图,正六边形ABCDEF能由△ABO平移得到的图形有哪几个?
如图,正六边形ABCDEF能由△ABO平移得到的图形有哪几个?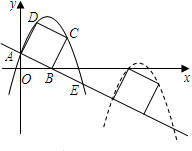 如图,已知直线y=-2x+2交坐标轴于A,B两点,以线段AB为边向上作矩形ABCD,AB:AD=1:2,过点A,D,C的抛物线与直线另一个交点为E.
如图,已知直线y=-2x+2交坐标轴于A,B两点,以线段AB为边向上作矩形ABCD,AB:AD=1:2,过点A,D,C的抛物线与直线另一个交点为E.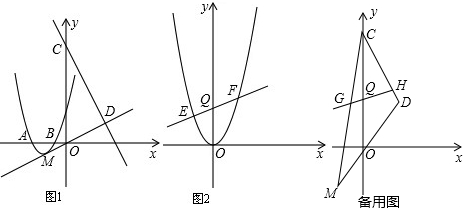
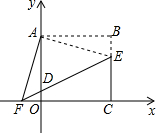 如图,在平面直角坐标系中,正方形OABC的点A在y轴上,点C在x轴上,点B(4,4),点E在BC边上,将△ABE绕点A顺时针旋转90°,得△AOF,连接EF交y轴于点D.
如图,在平面直角坐标系中,正方形OABC的点A在y轴上,点C在x轴上,点B(4,4),点E在BC边上,将△ABE绕点A顺时针旋转90°,得△AOF,连接EF交y轴于点D.