题目内容
2.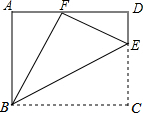 如图,点E是矩形ABCD中CD边上一点,△BCE沿BE折叠为△BFE,点F落在AD上.若sin∠DFE=$\frac{1}{3}$,则 tan∠EBC的值为$\frac{\sqrt{2}}{2}$.
如图,点E是矩形ABCD中CD边上一点,△BCE沿BE折叠为△BFE,点F落在AD上.若sin∠DFE=$\frac{1}{3}$,则 tan∠EBC的值为$\frac{\sqrt{2}}{2}$.
分析 首先证得△ABF∽△DFE,sin∠DFE=$\frac{1}{3}$,设DE=a,EF=3a,DF=$\sqrt{{EF}^{2}{-DE}^{2}}$=2$\sqrt{2}$a,可得出CE=EF=3a,CD=DE+CE=4a,AB=4a,∠EBC=∠EBF,由△ABF∽△DFE,可得tan∠EBC=tan∠EBF=$\frac{EF}{BE}$=$\frac{\sqrt{2}}{2}$.
解答 解:∵四边形ABCD是矩形,
∴∠A=∠D=∠C=90°,
∵△BCE沿BE折叠为△BFE,
∴∠BFE=∠C=90°,
∴∠AFB+∠DFE=180°-∠BFE=90°,
又∵∠AFB+∠ABF=90°,
∴∠ABF=∠DFE,
∴△ABF∽△DFE,
在Rt△DEF中,sin∠DFE=$\frac{DE}{EF}$=$\frac{1}{3}$,
∴设DE=a,EF=3a,DF=$\sqrt{{EF}^{2}{-DE}^{2}}$=2$\sqrt{2}$a,
∵△BCE沿BE折叠为△BFE,
∴CE=EF=3a,CD=DE+CE=4a,AB=4a,∠EBC=∠EBF,
∵△ABF∽△DFE,
∴$\frac{EF}{BF}=\frac{DF}{AB}=\frac{2\sqrt{2}a}{4a}$=$\frac{\sqrt{2}}{2}$,
∴tan∠EBF=$\frac{EF}{BF}$=$\frac{\sqrt{2}}{2}$,
tan∠EBC=tan∠EBF=$\frac{\sqrt{2}}{2}$.
故答案为:$\frac{\sqrt{2}}{2}$.
点评 本题主要考查了矩形的性质以及相似三角形的证明方法,以及直角三角形中角的函数值,找到等角代换是解答此题的关键.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
14. 如图,将一块含有30°角的直角三角板的两个顶点叠放在矩形的两条对边上,如果∠1=25°,那么∠2的度数是( )
如图,将一块含有30°角的直角三角板的两个顶点叠放在矩形的两条对边上,如果∠1=25°,那么∠2的度数是( )
 如图,将一块含有30°角的直角三角板的两个顶点叠放在矩形的两条对边上,如果∠1=25°,那么∠2的度数是( )
如图,将一块含有30°角的直角三角板的两个顶点叠放在矩形的两条对边上,如果∠1=25°,那么∠2的度数是( )| A. | 53° | B. | 55° | C. | 57° | D. | 60° |
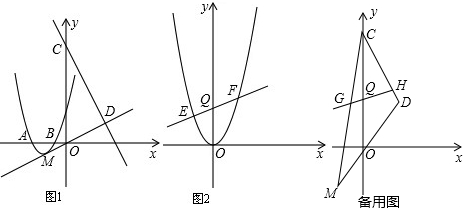
11.已知方程x2+mx+n=0的两根为x1、x2(x1<x2),方程x2+mx+n-1=0的两根为x3、x4(x3<x4),则下列关系一定成立的是( )
| A. | x1<x2<x3<x4 | B. | x1<x3<x4<x2 | C. | x3<x4<x1<x2 | D. | x3<x1<x2<x4 |
12.计算1232-124×122=( )
| A. | -1 | B. | 1 | C. | 0 | D. | 2 |
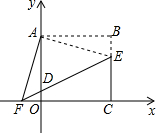 如图,在平面直角坐标系中,正方形OABC的点A在y轴上,点C在x轴上,点B(4,4),点E在BC边上,将△ABE绕点A顺时针旋转90°,得△AOF,连接EF交y轴于点D.
如图,在平面直角坐标系中,正方形OABC的点A在y轴上,点C在x轴上,点B(4,4),点E在BC边上,将△ABE绕点A顺时针旋转90°,得△AOF,连接EF交y轴于点D.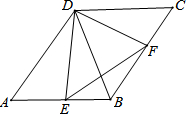 如图,在?ABCD中,∠A=60°,DE⊥AB,DF⊥BC,垂足分别为点E,F,有下列结论:
如图,在?ABCD中,∠A=60°,DE⊥AB,DF⊥BC,垂足分别为点E,F,有下列结论: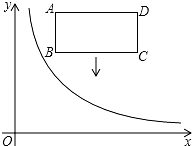 如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(x>0)的图象和矩形ABCD在第一象限,AD平行于x轴,且AB=2,AD=4,点A的坐标为(2,6).将矩形ABCD向下平移,平移后的矩形记为A′B′C′D′在平移过程中,有两个顶点恰好落在反比例函数图象上.
如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(x>0)的图象和矩形ABCD在第一象限,AD平行于x轴,且AB=2,AD=4,点A的坐标为(2,6).将矩形ABCD向下平移,平移后的矩形记为A′B′C′D′在平移过程中,有两个顶点恰好落在反比例函数图象上.