题目内容
5.如图,在矩形ABCD中,AB=$2\sqrt{3}$,BC=8,M是BC 的中点,P、Q两点同时从M点出发,其中点P以每秒1个单位的速度向B运动,到达点B后立即按原来的速度反向向M点运动,到达M点后停止,点Q以每秒1个单位的速度沿射线MC运动,当点P停止时点Q也随之停止.以PQ为边长向上作等边三角形PQE.(1)求点E落在线段AD上时,P、Q两点的运动时间;
(2)设运动时间为t秒,矩形ABCD与△PQE重叠的面积为S,求出S与t之间的函数关系式,并写出t的取值范围;
(3)在矩形ABCD中,点N是线段BC上一点,并且CN=2,在直线CD上找一点H(H点在D点的上方)连接HN,DN,将△HDN绕点N逆时针旋转90°,得到△H′D′N,连接HH',得到四边形HH′D′N,四边形HH′D′N的面积能否是$\frac{31}{2}-\sqrt{3}$?若能,求出HD的长;若不能,请说明理由.

分析 (1)当点E落在线段AD上时,由△EPQ是等边三角形,得到△EPM是直角三角形,根据勾股定理列方程解出t的值;
(2)分类讨论;当0≤t≤2时,因为△EPQ是等边三角形,如图1,得到PM=QM=t,EM⊥PQ,PQ=2t,EM=$\sqrt{3}$t,根据三角形的面积公式即可求出S=$\frac{1}{2}$PQ•EM=$\sqrt{3}$t2,当2<t≤4,如图2,因为PQ=2t,EM=$\sqrt{3}$t,PF=4,得到FG=2t-4,根据图形面积的和差可求出S=S△EPQ-S△EFG=$\frac{1}{2}$•2t$•\sqrt{3}t$-$\frac{1}{2}$(2t-4)($\sqrt{3}$t-2$\sqrt{3}$)=4$\sqrt{3}$t-4$\sqrt{3}$,当4<t≤6,如图3,由题意得到PQ=8,FG=4,DG=6-t,CQ=t-4,根据图形面积的和差可求出S=S△EPQ-S△EFG-S△GDN-S△CQN=-$\sqrt{3}$t2$+10\sqrt{3}t$-2$\sqrt{3}$,当6<t≤8时,如图4,根据题意得PQ=8,FG=4,DF=10-t,CP=12-t,由梯形的面积公式即可得到S=S四边形PCDF=$\frac{1}{2}$(10-t+12-t)×$2\sqrt{3}$=-2$\sqrt{3}$t+22$\sqrt{3}$;
(3)由旋转的性质得到△H′NH是等腰直角三角形,根据图形面积的和差即可求出结果.
解答 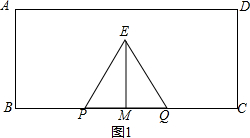 解:(1)当点E落在线段AD上时,△EPQ是等边三角形,
解:(1)当点E落在线段AD上时,△EPQ是等边三角形,
∴EM⊥PQ,PM=QM,
∴EM=AB=2$\sqrt{3}$,PM=MQ=t,
∴PQ=EP=EQ=2t,
∴t2${+(2\sqrt{3})}^{2}$=(2t)2,
∴t=2(负值舍去),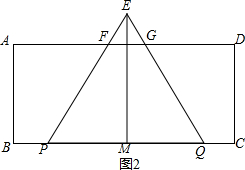
∴点E落在线段AD上时,P、Q两点的运动时间为:2s;
(2)当0≤t≤2时,∵△EPQ是等边三角形,如图1,
∴PM=QM=t,EM⊥PQ,
∴PQ=2t,EM=$\sqrt{3}$t,
∴S=$\frac{1}{2}$PQ•EM=$\sqrt{3}$t2,
当2<t≤4,如图2,
∵PQ=2t,EM=$\sqrt{3}$t,PF=4,
∴FG=2t-4,
∴S=S△EPQ-S△EFG=$\frac{1}{2}$•2t$•\sqrt{3}t$-$\frac{1}{2}$(2t-4)($\sqrt{3}$t-2$\sqrt{3}$)=4$\sqrt{3}$t-4$\sqrt{3}$,
当4<t≤6,如图3,
PQ=8,FG=4,DG=6-t,CQ=t-4,
∴S=S△EPQ-S△EFG-S△GDN-S△CQN
=$\frac{1}{2}$×$8×4\sqrt{3}$-$\frac{1}{2}×4×2\sqrt{3}$-$\frac{\sqrt{3}}{2}$(6-t)2-$\frac{\sqrt{3}}{2}$(t-4)2
=-$\sqrt{3}$t2$+10\sqrt{3}t$-2$\sqrt{3}$,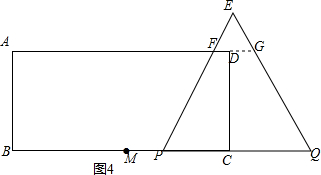
当6<t≤8时,如图4,
PQ=8,FG=4,DF=10-t,CP=12-t,
∴S=S四边形PCDF=$\frac{1}{2}$(10-t+12-t)×$2\sqrt{3}$=-2$\sqrt{3}$t+22$\sqrt{3}$,
综上所述:S=$\left\{\begin{array}{l}{{\sqrt{3}t}^{2}(0≤t≤2)}\\{4\sqrt{3}t-4\sqrt{3}(2<t≤4)}\\{-{\sqrt{3}t}^{2}+10\sqrt{3}t-2\sqrt{3}(4<t≤6)}\\{-2\sqrt{3}t+22\sqrt{3}(6<t≤8)}\end{array}\right.$,
(3)设HD=x,则NH2=${(x+2\sqrt{3})}^{2}$+22=x2$+4\sqrt{3}x$+16,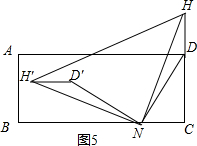
∵△H′NH是等腰直角三角形,
∴S四边形HH′D′N=S△HH′N-S△D′H′N=${\frac{1}{2}NH}^{2}$-$\frac{1}{2}$•HD•NC=$\frac{1}{2}$(${x}^{2}+4\sqrt{3}x+16$)-$\frac{1}{2}×2•x$=$\frac{31}{2}$-$\sqrt{3}$,
x2+(4$\sqrt{3}$-2)x+(2$\sqrt{3}$-15)=0,
解得:x=$\sqrt{3}$或x=2+5$\sqrt{3}$,
∴HD=$\sqrt{3}$或HD=2+$\sqrt{5}$.
点评 本题考查了等边三角形的性质,勾股定理,三角形的面积的求法,旋转的性质,特别是要注意进行分类讨论.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 如图,将一块含有30°角的直角三角板的两个顶点叠放在矩形的两条对边上,如果∠1=25°,那么∠2的度数是( )
如图,将一块含有30°角的直角三角板的两个顶点叠放在矩形的两条对边上,如果∠1=25°,那么∠2的度数是( )| A. | 53° | B. | 55° | C. | 57° | D. | 60° |
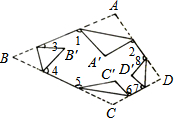 如图所示,把一个四边形纸片ABCD的四个顶角分别向内折叠,折叠之后,4个顶点不重合,那么图中∠1+∠2+∠3+∠4+∠5+∠6+∠7+∠8的度数是( )
如图所示,把一个四边形纸片ABCD的四个顶角分别向内折叠,折叠之后,4个顶点不重合,那么图中∠1+∠2+∠3+∠4+∠5+∠6+∠7+∠8的度数是( )| A. | 540° | B. | 630° | C. | 720° | D. | 810° |
 如图,正六边形ABCDEF能由△ABO平移得到的图形有哪几个?
如图,正六边形ABCDEF能由△ABO平移得到的图形有哪几个?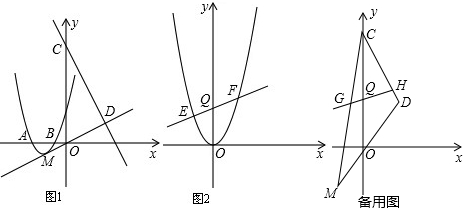
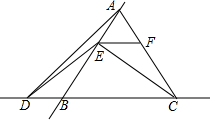 已知:△ABC是正三角形,且边长为1,点E是直线AB上的一个动点,过点E作BC的平行线交直线AC于点F,将线段EC绕点E旋转,使点C落在直线BC上的点D处;
已知:△ABC是正三角形,且边长为1,点E是直线AB上的一个动点,过点E作BC的平行线交直线AC于点F,将线段EC绕点E旋转,使点C落在直线BC上的点D处;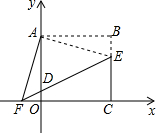 如图,在平面直角坐标系中,正方形OABC的点A在y轴上,点C在x轴上,点B(4,4),点E在BC边上,将△ABE绕点A顺时针旋转90°,得△AOF,连接EF交y轴于点D.
如图,在平面直角坐标系中,正方形OABC的点A在y轴上,点C在x轴上,点B(4,4),点E在BC边上,将△ABE绕点A顺时针旋转90°,得△AOF,连接EF交y轴于点D.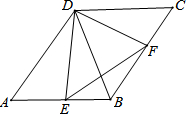 如图,在?ABCD中,∠A=60°,DE⊥AB,DF⊥BC,垂足分别为点E,F,有下列结论:
如图,在?ABCD中,∠A=60°,DE⊥AB,DF⊥BC,垂足分别为点E,F,有下列结论: