题目内容
15.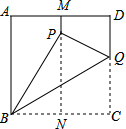 如图,有一张面积为3的正方形纸片ABCD,M,N分别是AD,BC边的中点,将C点折叠至MN上,落在P点的位置,折痕为BQ,连结PQ,则PQ=1.
如图,有一张面积为3的正方形纸片ABCD,M,N分别是AD,BC边的中点,将C点折叠至MN上,落在P点的位置,折痕为BQ,连结PQ,则PQ=1.
分析 根据正方形的面积求出边长,根据翻折的性质可得BP=BC,PQ=CQ,过点Q作QE⊥MN于E,可得四边形NCQE是矩形,利用勾股定理列式求出PN,再求CN,设CQ=x,表示出PQ、PE,然后利用勾股定理列方程求出PQ.
解答 解:∵正方形纸片ABCD的面积为3,
∴正方形的边长为$\sqrt{3}$,
由翻折的性质得,BP=BC=$\sqrt{3}$,PQ=CQ,
过点Q作QE⊥MN于E,则四边形NCQE是矩形,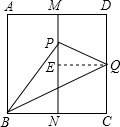
在Rt△PBN中,由勾股定理得,PN=$\sqrt{(\sqrt{3})^{2}-(\frac{\sqrt{3}}{2})^{2}}$=$\frac{3}{2}$,
∵M,N分别是AD,BC边的中点,
∴CN=$\frac{\sqrt{3}}{2}$
设CQ=x,则PQ=CQ=x,PE=$\frac{3}{2}$-x,
在Rt△PEQ中,由勾股定理得,PE2+EQ2=PQ2,
即($\frac{3}{2}$-x)2+($\frac{\sqrt{3}}{2}$)2=x2,
解得x=1.
故答案为:1.
点评 本题考查了翻折变换的性质,勾股定理,熟记性质并利用勾股定理列出方程是解题的关键,本题难点在于作辅助线构造出直角三角形并两次利用勾股定理.

练习册系列答案
相关题目
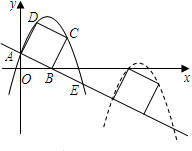 如图,已知直线y=-2x+2交坐标轴于A,B两点,以线段AB为边向上作矩形ABCD,AB:AD=1:2,过点A,D,C的抛物线与直线另一个交点为E.
如图,已知直线y=-2x+2交坐标轴于A,B两点,以线段AB为边向上作矩形ABCD,AB:AD=1:2,过点A,D,C的抛物线与直线另一个交点为E.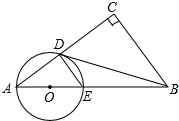 已知:如图,在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC,AB分别交于点D,E,连接DE、DB,若∠CBD=∠A.
已知:如图,在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC,AB分别交于点D,E,连接DE、DB,若∠CBD=∠A.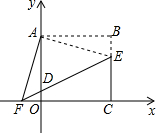 如图,在平面直角坐标系中,正方形OABC的点A在y轴上,点C在x轴上,点B(4,4),点E在BC边上,将△ABE绕点A顺时针旋转90°,得△AOF,连接EF交y轴于点D.
如图,在平面直角坐标系中,正方形OABC的点A在y轴上,点C在x轴上,点B(4,4),点E在BC边上,将△ABE绕点A顺时针旋转90°,得△AOF,连接EF交y轴于点D.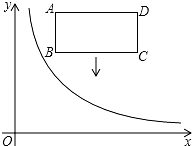 如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(x>0)的图象和矩形ABCD在第一象限,AD平行于x轴,且AB=2,AD=4,点A的坐标为(2,6).将矩形ABCD向下平移,平移后的矩形记为A′B′C′D′在平移过程中,有两个顶点恰好落在反比例函数图象上.
如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(x>0)的图象和矩形ABCD在第一象限,AD平行于x轴,且AB=2,AD=4,点A的坐标为(2,6).将矩形ABCD向下平移,平移后的矩形记为A′B′C′D′在平移过程中,有两个顶点恰好落在反比例函数图象上. 如图,直线AB平行于CD,直线l分别于AB、CD相交于点M、N,若∠1=130°,则∠2=50°.
如图,直线AB平行于CD,直线l分别于AB、CD相交于点M、N,若∠1=130°,则∠2=50°.