题目内容
19.抛物线y=$\frac{1}{2}$x2-2x+m与x轴只有一个公共点,把抛物线向下平移使之过原点后,与x轴的另一个交点为A,顶点为M,求△OAM的面积.分析 因为抛物线y=$\frac{1}{2}$x2-2x+m与x轴只有一个公共点,所以△=0,求出m=2,写出解析式,向下平移2个单位后过原点,则平移后的解析式为:y=$\frac{1}{2}$x2-2x,顶点坐标M(2,-2),与x轴另一交点A(4,0),根据三角形面积公式求出△OAM的面积.
解答 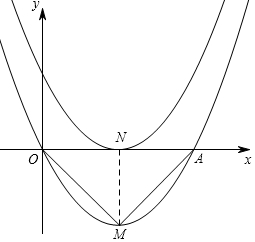 解:△=(-2)2-4×$\frac{1}{2}$m=0,
解:△=(-2)2-4×$\frac{1}{2}$m=0,
m=2,
∴抛物线解析式为:y=$\frac{1}{2}$x2-2x+2,
与y轴交于点(0,2),
所以把抛物线向下平移使之过原点,则向下平移2个单位,
得抛物线的解析式为:y=$\frac{1}{2}$x2-2x=$\frac{1}{2}$(x2-4x+4-4)=$\frac{1}{2}$(x-2)2-2,
∴顶点M(2,-2),
当y=0时,$\frac{1}{2}$x2-2x=0,
x(x-4)=0,
x1=0,x2=4,
∴A(4,0),
过M作MN⊥x轴于N,
∴S△OAM=$\frac{1}{2}$OA•MN=$\frac{1}{2}$×4×2=4.
点评 本题考查了二次函数图象与x轴交点问题及几何变换问题,明确抛物线与x轴交点的个数与△=b2-4ac的关系:①△=b2-4ac>0时,抛物线与x轴有2个交点;②△=b2-4ac=0时,抛物线与x轴有1个交点;③△=b2-4ac<0时,抛物线与x轴没有交点.还要知道抛物线过原点,则常数顶为0或经过(0,0),平移前后的抛物线解析式二次项系数不变.

练习册系列答案
相关题目
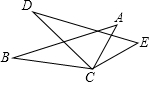 如图,已知∠B=∠D,AB=DE,要推得△ABC≌△EDC;
如图,已知∠B=∠D,AB=DE,要推得△ABC≌△EDC;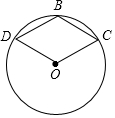 已知,如图,点B、C、D在⊙O上,四边形OCBD是平行四边形,
已知,如图,点B、C、D在⊙O上,四边形OCBD是平行四边形,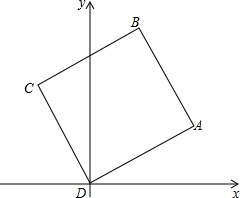 正方形ABCD如图放置,D与原点重合,C在第二象限,A点坐标为(8,4).
正方形ABCD如图放置,D与原点重合,C在第二象限,A点坐标为(8,4).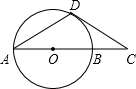 如图,AB是⊙O的直径,AD是⊙O的弦,过点D作⊙O的切线与AB的延长线交于点C,若∠CAD=30°,求证:AD=CD.
如图,AB是⊙O的直径,AD是⊙O的弦,过点D作⊙O的切线与AB的延长线交于点C,若∠CAD=30°,求证:AD=CD. 如图,矩形ABCD中,CE平分∠BCD交AD于F,AE⊥CE于E,连BE交AD于N,连BD交CE于M,若CE=CB,则下列结论:①△AEF≌△CDF;②N为BE的黄金分割点;③S△MBC=(3+2$\sqrt{2}$)S△NEA;④BD=$\sqrt{2}$BE;其中正确结论个数是( )
如图,矩形ABCD中,CE平分∠BCD交AD于F,AE⊥CE于E,连BE交AD于N,连BD交CE于M,若CE=CB,则下列结论:①△AEF≌△CDF;②N为BE的黄金分割点;③S△MBC=(3+2$\sqrt{2}$)S△NEA;④BD=$\sqrt{2}$BE;其中正确结论个数是( )