Question

14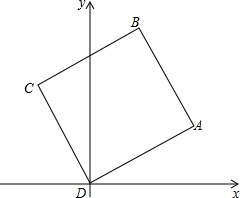．正方形ABCD如图放置，D与原点重合，C在第二象限，A点坐标为（8，4）．
求：（1）求B点坐标；
（2）求C点坐标．

Answer 1

分析 （1）首先过点A作AM⊥x轴于点M，过点C作CN⊥x轴于点N，易证得△ADM≌△DCN（AAS），则可求得点C的坐标，又由线段AB是线段CD向右平移8个单位长度，向上平移4个单位长度得到的，即可求得B点坐标；
（2）由（1）即可求得答案．

解答 解：（1）过点A作AM⊥x轴于点M，过点C作CN⊥x轴于点N，
∴∠AMD=∠CND=90°，
∴∠ADM+∠DAM=90°，
∵四边形ABCD是正方形，
∴∠ADC=90°，AD=CD，AB∥CD，AB=CD，
∴∠ADM+∠CDN=90°，
∴∠DAM=∠CDN，
在△ADM和△DCN中，
$\left\{\begin{array}{l}{∠AMD=∠DNC}\\{∠DAM=∠CDN}\\{AD=DC}\end{array}\right.$，
∴△ADM≌△DCN（AAS），
∴AM=DN=4，CN=DM=8，
∴点C的坐标为：（-4，8）；
∵AB∥CD，AB=CD，
∴线段AB是线段CD向右平移8个单位长度，向上平移4个单位长度得到的，
∴B的坐标为：（4，12）．

（2）由（1）得点C的坐标为：（-4，8）．

点评 此题考查了正方形的性质、全等三角形的判定与性质以及点与坐标的关系．注意准确作出辅助线是解此题的关键．