题目内容
7.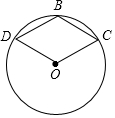 已知,如图,点B、C、D在⊙O上,四边形OCBD是平行四边形,
已知,如图,点B、C、D在⊙O上,四边形OCBD是平行四边形,(1)求证:$\widehat{BC}$=$\widehat{BD}$;
(2)若⊙O的半径为2,求$\widehat{BD}$的长.
分析 (1)连接OB,如图,利用平行四边形的性质得OC=BD,OD=BC,然后利用OC=OD得到BD=BC,然后根据弦、弧和圆心角的关系得到$\widehat{BC}$=$\widehat{BD}$;
(2)先判断△OBD和△OBC为等边三角形,则∠BOC=∠BOD=60°,所以∠COD=120°,然后利用弧长公式计算$\widehat{BD}$的长.
解答 (1)证明: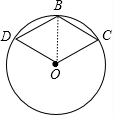 连接OB,如图,
连接OB,如图,
∵四边形OCBD是平行四边形,
∴OC=BD,OD=BC,
而OC=OD,
∴BD=BC,
∴$\widehat{BC}$=$\widehat{BD}$;
(2)解:∵OD=BD=OB=OC=BC=2,
∴△OBD和△OBC为等边三角形,
∴∠BOC=∠BOD=60°,
∴∠COD=120°,
∴$\widehat{BD}$的长=$\frac{120•π•2}{180}$=$\frac{4}{3}$π.
点评 本题考查了弧长公式:圆周长公式:C=2πR;弧长公式:l=$\frac{nπR}{180}$(弧长为l,圆心角度数为n,圆的半径为R).也考查了平行四边形的性质和等边三角形的判定与性质.

练习册系列答案
相关题目
2.若圆的一条弦把圆分成度数比为1:2的两条弧,则优弧所对的圆周角为( )
| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
2.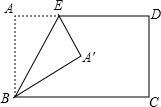 如图,将矩形ABCD沿BE折叠,点A落在点A′处,若∠CBA′=30°,则∠BEA′等于( )
如图,将矩形ABCD沿BE折叠,点A落在点A′处,若∠CBA′=30°,则∠BEA′等于( )
 如图,将矩形ABCD沿BE折叠,点A落在点A′处,若∠CBA′=30°,则∠BEA′等于( )
如图,将矩形ABCD沿BE折叠,点A落在点A′处,若∠CBA′=30°,则∠BEA′等于( )| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
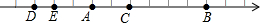 如图,图中数轴的单位长度为1.请回答下列问题:
如图,图中数轴的单位长度为1.请回答下列问题: