题目内容
14. 如图,矩形ABCD中,CE平分∠BCD交AD于F,AE⊥CE于E,连BE交AD于N,连BD交CE于M,若CE=CB,则下列结论:①△AEF≌△CDF;②N为BE的黄金分割点;③S△MBC=(3+2$\sqrt{2}$)S△NEA;④BD=$\sqrt{2}$BE;其中正确结论个数是( )
如图,矩形ABCD中,CE平分∠BCD交AD于F,AE⊥CE于E,连BE交AD于N,连BD交CE于M,若CE=CB,则下列结论:①△AEF≌△CDF;②N为BE的黄金分割点;③S△MBC=(3+2$\sqrt{2}$)S△NEA;④BD=$\sqrt{2}$BE;其中正确结论个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 先利用矩形的性质和角平分线的性质判断出△CDF和△AEF是全等的等腰直角三角形,判断出①正确,设出EG=x,利用平行线得出比例式$\frac{EG}{BN}=\frac{EG}{AB}=\frac{1}{\sqrt{2}}$,判断出②错误,再利用勾股定理和相似三角形的性质,用x表示出BC,PC,AN,即可求出三角形NEA和三角形BMC的面积,即可判断出③正确,最后用勾股定理求出BD和BE可判断出④正确.
解答 解:如图,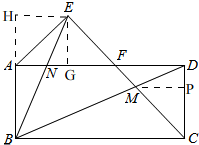
∵四边形ABCD是矩形,
∴AB=CB,AD=BC,∠CBD=∠ABC=∠ADC=∠BAD=90°,AD∥BC
∵CE平分∠BCD交AD于F,
∴∠DCF=∠BCF=45°,
∴∠AFE=∠CFD=∠BCF=45°,
∵AE⊥CF,
∴∠AEF=∠CDF=90°,
∵CE=CB,
∴∠CBE=∠CEB=$\frac{1}{2}$(180°-45°)=67.5°,
∴∠AEB=∠ABE,
∴AE=AB=CD,
在△AEF和△CDF中,$\left\{\begin{array}{l}{∠AFE=∠CFD}\\{∠AEF=∠CDF}\\{AE=CD}\end{array}\right.$,
∴△AEF≌△CDF,
所以①正确;
∵△AEF≌△CDF,
∴∠EAF=45°,
过点E作EG⊥AD
设EG=x,
∴AG=x,AE=AB=DF=CD=$\sqrt{2}$x,AF=2x
∵EG∥AB,
∴$\frac{EG}{BN}=\frac{EG}{AB}=\frac{1}{\sqrt{2}}$,
∴N不是BE的黄金分割点;
∴所以②错误;
∵EG∥AB,
∴$\frac{NG}{AN}=\frac{EG}{AB}=\frac{1}{\sqrt{2}}$,
∵AG=x,
∴AN=(2-$\sqrt{2}$)x,
∴S△NEA=$\frac{1}{2}$AN×EG=$\frac{2-\sqrt{2}}{2}$x2,
∵CF=AF=$\sqrt{2}$x,EF=x,
∴BC=CE=($\sqrt{2}$+2)x,
过点M作MP⊥CD,
∴$\frac{DP}{PC}=\frac{DF}{BC}$=$\frac{x}{(\sqrt{2}+1)x}$=$\frac{1}{\sqrt{2}+1}$,
∵CD=PC+PD=$\sqrt{2}$x,
∴PC=$\frac{\sqrt{2}}{2}$x,
∴S△BMC=$\frac{1}{2}$BC×PC=$\frac{2+\sqrt{2}}{2}$x2,
∴S△MBC=(3+2$\sqrt{2}$)S△NEA;
所以③正确;
过点E作EH⊥AB交BA延长线于H,
∴四边形AGEH是正方形,
∴AH=HE=EG=x,
在Rt△BHE中,BH-AB+AH=($\sqrt{2}$+1)x,EH=x,
∴BE2=BH2+HE2=(4+2$\sqrt{2}$)x2=2(2+$\sqrt{2}$)x2,
在Rt△BCD中,CD=$\sqrt{2}$x,BC=(2+$\sqrt{2}$)x,
∴BD2=BC2+CD2=(8+4$\sqrt{2}$)x2=4(2+$\sqrt{2}$)x2=2BE2,
∴BD=$\sqrt{2}$BE;
所以④正确,
即:正确的有①③④共3个,
故选C.
点评 此题是三角形综合题,主要考查了角平分线的定义,矩形的性质,等腰直角三角形的判定和性质,全等三角形的判定和性质,勾股定理,解本题的关键是判断出AB=AE和用勾股定理表示线段,难点是作出辅助线.是一道难度比较大的中考压轴题.

 阅读快车系列答案
阅读快车系列答案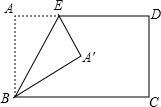 如图,将矩形ABCD沿BE折叠,点A落在点A′处,若∠CBA′=30°,则∠BEA′等于( )
如图,将矩形ABCD沿BE折叠,点A落在点A′处,若∠CBA′=30°,则∠BEA′等于( )| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
| A. | $\sqrt{2}-\sqrt{3}$ | B. | 2$-\sqrt{3}$ | C. | 3$\sqrt{2}$-2$\sqrt{3}$ | D. | $\sqrt{2}$ |
 已知,如图,在△ABC中,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC外,若∠2=25°,则∠1的度数为105°.
已知,如图,在△ABC中,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC外,若∠2=25°,则∠1的度数为105°. 如图,在?ABCD中,E为CD中点,AE与BD相交于点O,S△DOE=15cm2,则S△AOB等于60cm2.
如图,在?ABCD中,E为CD中点,AE与BD相交于点O,S△DOE=15cm2,则S△AOB等于60cm2.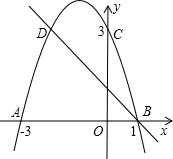 如图,二次函数的图象与x轴相交于A(-3,0)、B(1,0)两点,与y轴相交于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.
如图,二次函数的图象与x轴相交于A(-3,0)、B(1,0)两点,与y轴相交于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D. 四边形ABCD为梯形其中AB∥CD,∠AEG=∠CEH,AF=CF,求证:四边形EGFH为平行四边形.
四边形ABCD为梯形其中AB∥CD,∠AEG=∠CEH,AF=CF,求证:四边形EGFH为平行四边形.