题目内容
10.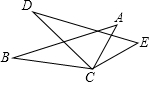 如图,已知∠B=∠D,AB=DE,要推得△ABC≌△EDC;
如图,已知∠B=∠D,AB=DE,要推得△ABC≌△EDC;(1)若以“SAS”为依据,则可添加条件BC=DC;(写一个即可,以下同)
(2)若以“ASA”为依据,则可添加条件∠A=∠E;
(3)若以“AAS”为依据,则可添加条件∠ACB=∠ECD.
分析 (1)根据全等三角形的判定定理SAS,结合给定条件以及图形即可找出另一对相等的边;
(2)根据全等三角形的判定定理ASA,结合给定条件以及图形即可找出另一对相等的角;
(3)根据全等三角形的判定定理AAS,结合给定条件以及图形即可找出另一对相等的角.
解答 解:(1)∵∠B=∠D,AB=ED,
当BC=DC时,在△ABC和△EDC中,$\left\{\begin{array}{l}{AB=ED}\\{∠B=∠D}\\{BC=DC}\end{array}\right.$,
∴△ABC≌△EDC(SAS).
故答案为:BC=DC.
(2)∵∠B=∠D,AB=ED,
当∠A=∠E时,在△ABC和△EDC中,$\left\{\begin{array}{l}{∠B=∠D}\\{AB=ED}\\{∠A=∠E}\end{array}\right.$,
∴△ABC≌△EDC(ASA).
故答案为:∠A=∠E.
(3)∵∠B=∠D,AB=ED,
当∠ACB=∠ECD时,在△ABC和△EDC中,$\left\{\begin{array}{l}{∠B=∠D}\\{∠ACB=∠ECD}\\{AB=ED}\end{array}\right.$,
∴△ABC≌△EDC(AAS).
故答案为:∠ACB=∠ECD.
点评 本题考查了全等三角形的判定,熟练掌握全等三角形的各判定定理是解题的关键.

练习册系列答案
相关题目
20.若x<y,化简|y-x|-$\sqrt{(x-y)^{2}}$的结果是( )
| A. | 2y-2x | B. | -2x | C. | 2y | D. | 0 |
5.小玉做以下4道计算题,①-12004=1,②0-|-1|=1,③$\frac{1}{2}$÷(-$\frac{1}{2}$)=-1,④-$\frac{1}{2}$+$\frac{2}{3}$=$\frac{1}{6}$,则正确的有( )
| A. | 1道 | B. | 2道 | C. | 3道 | D. | 4道 |
2.若圆的一条弦把圆分成度数比为1:2的两条弧,则优弧所对的圆周角为( )
| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
 A、B两市相距260千米,甲车从A市前往B市运送物资,行驶2小时到达M地,发现汽车出现故障,立即通知技术人员乘乙车从A市赶来维修(通知时间不计),乙车到达M地后用20分钟修好甲车,又以原速原路返回,同时甲车以原来1.5倍的速度前往B市.如图时两车相距A市的路程y(单位:千米)与甲车行驶时间(单位:小时)之间的函数图象,下列四中说法:
A、B两市相距260千米,甲车从A市前往B市运送物资,行驶2小时到达M地,发现汽车出现故障,立即通知技术人员乘乙车从A市赶来维修(通知时间不计),乙车到达M地后用20分钟修好甲车,又以原速原路返回,同时甲车以原来1.5倍的速度前往B市.如图时两车相距A市的路程y(单位:千米)与甲车行驶时间(单位:小时)之间的函数图象,下列四中说法: 已知,如图,在△ABC中,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC外,若∠2=25°,则∠1的度数为105°.
已知,如图,在△ABC中,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC外,若∠2=25°,则∠1的度数为105°.