题目内容
4.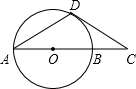 如图,AB是⊙O的直径,AD是⊙O的弦,过点D作⊙O的切线与AB的延长线交于点C,若∠CAD=30°,求证:AD=CD.
如图,AB是⊙O的直径,AD是⊙O的弦,过点D作⊙O的切线与AB的延长线交于点C,若∠CAD=30°,求证:AD=CD.
分析 连接OD,如图,先利用OA=OD得到∠ODA=∠OAD=30°,则利用三角形外角性质得∠COD=60°,再根据切线的性质得∠ODC=90°,所以∠C=30°,则可判断∠A=∠C,然后根据等腰三角形的判定方法可得AD=CD.
解答 证明:连接OD,如图,
∵OA=OD,
∴∠ODA=∠OAD=30°,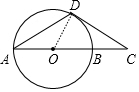
∴∠COD=∠OAD+∠ODA=60°,
∵CD为⊙O的切线,
∴OD⊥CD,
∴∠ODC=90°,
∴∠C=30°,
∴∠A=∠C,
∴AD=CD.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.简记作:见切点,连半径,见垂直.

练习册系列答案
相关题目
9. 如图,⊙O的半径为10,AB为弦,OC⊥AB,垂足为E.如果CE=4,那么AB的长是( )
如图,⊙O的半径为10,AB为弦,OC⊥AB,垂足为E.如果CE=4,那么AB的长是( )
 如图,⊙O的半径为10,AB为弦,OC⊥AB,垂足为E.如果CE=4,那么AB的长是( )
如图,⊙O的半径为10,AB为弦,OC⊥AB,垂足为E.如果CE=4,那么AB的长是( )| A. | 8 | B. | 12 | C. | 16 | D. | 20 |
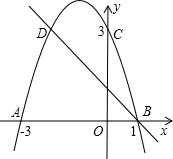 如图,二次函数的图象与x轴相交于A(-3,0)、B(1,0)两点,与y轴相交于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.
如图,二次函数的图象与x轴相交于A(-3,0)、B(1,0)两点,与y轴相交于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.