题目内容
8.约分:(1)$\frac{2x+{x}^{2}}{2x}$;
(2)$\frac{{a}^{2}b+a{b}^{2}}{ab}$;
(3)$\frac{2ab+{b}^{2}}{4{a}^{2}+{b}^{2}+4ab}$;
(4)$\frac{{m}^{2}-4mn+4{n}^{2}}{{m}^{2}-4{n}^{2}}$.
分析 根据约分的步骤找出分子与分母的公分母,再约去即可.
解答 解:(1)$\frac{2x+{x}^{2}}{2x}=\frac{2+x}{2}=1+\frac{x}{2}$;
(2)$\frac{{a}^{2}b+a{b}^{2}}{ab}=a+b$;
(3)$\frac{2ab+{b}^{2}}{4{a}^{2}+{b}^{2}+4ab}=b$;
(4)$\frac{{m}^{2}-4mn+4{n}^{2}}{{m}^{2}-4{n}^{2}}=\frac{m-2n}{m+2n}$.
点评 本题考查了约分,用到的知识点是分式的基本性质,约去分式的分子与分母的公因式,不改变分式的值,这样的分式变形叫做分式的约分.确定公因式要分为系数、字母、字母的指数来分别确定.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.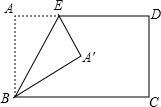 如图,将矩形ABCD沿BE折叠,点A落在点A′处,若∠CBA′=30°,则∠BEA′等于( )
如图,将矩形ABCD沿BE折叠,点A落在点A′处,若∠CBA′=30°,则∠BEA′等于( )
 如图,将矩形ABCD沿BE折叠,点A落在点A′处,若∠CBA′=30°,则∠BEA′等于( )
如图,将矩形ABCD沿BE折叠,点A落在点A′处,若∠CBA′=30°,则∠BEA′等于( )| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
3.化简$\frac{4}{\sqrt{2}}$-$\frac{\sqrt{6}}{\sqrt{3}}$的结果是( )
| A. | $\sqrt{2}-\sqrt{3}$ | B. | 2$-\sqrt{3}$ | C. | 3$\sqrt{2}$-2$\sqrt{3}$ | D. | $\sqrt{2}$ |
 已知,如图,在△ABC中,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC外,若∠2=25°,则∠1的度数为105°.
已知,如图,在△ABC中,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC外,若∠2=25°,则∠1的度数为105°.