题目内容
14.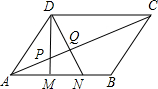 如图,在平行四边形ABCD中,M、N为AB的三等分点,DM、DN分别交AC于P、Q两点,则AP:PC=1:3,AP:PQ:CQ=5:3:12.
如图,在平行四边形ABCD中,M、N为AB的三等分点,DM、DN分别交AC于P、Q两点,则AP:PC=1:3,AP:PQ:CQ=5:3:12.
分析 根据平行四边形的性质知:AB=CD,则AM:CD=1:3,AN:CD=2:3;易证得△AMP∽△CDP,△ANQ∽△CDQ;进而可根据相似三角形的对应线段成比例求出AP、PC,AQ、QC的比例关系.
解答 解:∵四边形ABCD是平行四边形,
∴AB∥CD,且AB=CD;
∴△AMP∽△CDP,△ANQ∽△CDQ;
且AM:CD=1:3,AN:CD=2:3;
∴AP:PC=AM:CD=1:3,
∵△AMP∽△CDP,
∴AM:CD=AP:PC=AP:(PQ+QC)=$\frac{1}{3}$,即:3AP=PQ+QC,①
△ANQ∽△CDQ,
∴AN:CD=AQ:QC=(AP+PQ):QC=$\frac{2}{3}$,即2QC=3(AP+PQ),②
解①、②得:AQ=$\frac{2}{5}$AC,PQ=AQ-AP=$\frac{3}{20}$AC,QC=AC-AQ=$\frac{3}{5}$AC,
∴AP:PQ:QC=5:3:12.
故答案为:1:3,5:3:12.
点评 主要考查了三角形相似的性质和平行四边形的性质,要熟练掌握灵活运用.

练习册系列答案
相关题目
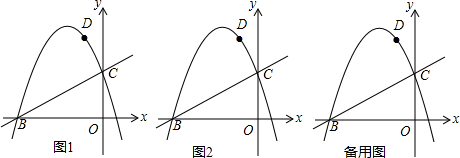
 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论: