题目内容
6.计算:(1)$\frac{{a}^{2}-4{b}^{2}}{3a{b}^{2}}$•$\frac{ab}{a-2b}$;
(2)$\frac{{x}^{2}-4{y}^{2}}{{x}^{2}+2xy+{y}^{2}}$÷$\frac{x+2y}{{x}^{2}+xy}$.
分析 (1)根据因式分解的方法,将分式的分子分母分解因式,再根据分式的乘法法则计算;
(2)根据因式分解的方法,将分式的分子分母分解因式,再根据分式的除法法则计算.
解答 解:(1)原式=$\frac{(a+2b)(a-2b)}{3a{b}^{2}}•\frac{ab}{a-2b}$=$\frac{a+2b}{3b}$;
(2)原式=$\frac{(x+2y)(x-2y)}{(x+y)^{2}}•\frac{x(x+y)}{x+2y}$=$\frac{{x}^{2}-2xy}{x+y}$.
点评 本题主要考查分式的乘除法法则,若分子分母是多项式时,要先分解因式,在根据法则计算,此题是常考题,要熟练掌握.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
11.下面是某射击队甲乙两名队员在一次队内射击选拔赛的成绩情况统计图.请利用图中提供的信息,解答下列问题:
(1)完成下表:
(2)根据图表信息,请你谈谈对这两名队员成绩的看法,并给教练组提出合理化建议(不超过50字)
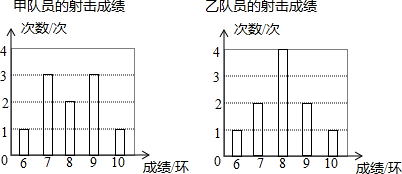
(1)完成下表:
| 姓名 | 平均成绩 | 众数 | 中位数 | 极差 | 方差 | 标准差 |
| 甲 | 8环 | 7环与9环 | 8环 | 4环 | 14 | $\sqrt{14}$ |
| 乙 | 8环 | 8环 | 8环 | 4环 | 12 | 2$\sqrt{3}$ |

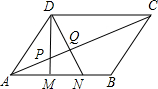 如图,在平行四边形ABCD中,M、N为AB的三等分点,DM、DN分别交AC于P、Q两点,则AP:PC=1:3,AP:PQ:CQ=5:3:12.
如图,在平行四边形ABCD中,M、N为AB的三等分点,DM、DN分别交AC于P、Q两点,则AP:PC=1:3,AP:PQ:CQ=5:3:12.