题目内容
15. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①b>0;②c=1;③b2-4ac>0;④a+b+c<0;⑤a-b+c>1
其中所有正确结论的序号是( )
| A. | ①② | B. | ①②③ | C. | ②③④ | D. | ②③④⑤ |
分析 根据开口方向、对称轴、抛物线与y轴的交点,确定a、b、c的符号,根据对称轴和图象确定y>0或y<0时,x的范围,确定代数式的符号
解答 解:∵开口向下,∴a<0,
∵对称轴在y轴的左侧和a<0,可知b<0,①错误;
∵抛物线与y轴交于(0,1),
∴c=1,②正确;
∵抛物线与x轴有两个交点,
∴b2-4ac>0,③正确;
∵当x=1时,y<0,
∴a+b+c<0,④正确;
∵当x=-1时,y有最大值,x=0时,y=1,
∴a-b+c>1,⑤正确
故选:D.
点评 本题考查的是二次函数图象与系数的关系,掌握二次函数的性质、灵活运用数形结合思想是解题的关键,解答时,要熟练运用抛物线上的点的坐标满足抛物线的解析式.

练习册系列答案
相关题目
3.一个不透明的袋子中装有若干个除颜色外均相同的小球,小明每次从袋子中摸出一个球,记录下颜色,然后放回,重复这样的试验1000次,记录结果如下:
(1)表格中a=0.71,b=0.70;
(2)估计从袋子中摸出一个球恰好是红球的概率约为0.7;(精确到0.1)
(3)如果袋子中有14个红球,那么袋子中除了红球,还有多少个其他颜色的球?
| 实验次数 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 1000 |
| 摸到红球次数m | 151 | 221 | 289 | 358 | 429 | 497 | 568 | 701 |
| 摸到红球频率$\frac{m}{n}$ | 0.75 | 0.74 | 0.72 | 0.72 | 0.72 | 0.71 | a | b |
(2)估计从袋子中摸出一个球恰好是红球的概率约为0.7;(精确到0.1)
(3)如果袋子中有14个红球,那么袋子中除了红球,还有多少个其他颜色的球?
10.函数y=$\sqrt{x-7}$中,自变量x的取值范围是( )
| A. | x>7 | B. | x≤7 | C. | x≥7 | D. | x<7 |
 如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:
如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法: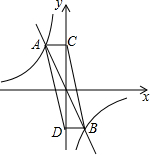 如图,直线y=kx(k<0)与双曲线y=$\frac{-2}{x}$交于点A、B,AC⊥y轴于C,BD⊥y轴于D,连接AD、BC,则四边形ABCD的面积为( )
如图,直线y=kx(k<0)与双曲线y=$\frac{-2}{x}$交于点A、B,AC⊥y轴于C,BD⊥y轴于D,连接AD、BC,则四边形ABCD的面积为( )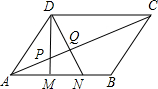 如图,在平行四边形ABCD中,M、N为AB的三等分点,DM、DN分别交AC于P、Q两点,则AP:PC=1:3,AP:PQ:CQ=5:3:12.
如图,在平行四边形ABCD中,M、N为AB的三等分点,DM、DN分别交AC于P、Q两点,则AP:PC=1:3,AP:PQ:CQ=5:3:12.