题目内容
16.用代入法解下列方程组:(1)$\left\{\begin{array}{l}{y=x+3}\\{7x+5y=9}\end{array}\right.$
(2)$\left\{\begin{array}{l}{3s-t=5}\\{5s+2t=15}\end{array}\right.$
(3)$\left\{\begin{array}{l}{4x+y=15}\\{3x-2y=3}\end{array}\right.$
(4)$\left\{\begin{array}{l}{4(x+2)+5y=1}\\{2x+3(y+2)=3}\end{array}\right.$.
分析 (1)把①代入②得出7x+5(x+3)=9,求出x,把x的值代入①求出y即可;
(2)①×2+②得出11s=25,求出s,把s的值代入①求出t即可;
(3)①×2+②得出11x=33,求出x,把x的值代入①求出y即可;
(4)整理后①-②×2得出-y=-1,求出y,把y的值入②求出x即可.
解答 解:(1)$\left\{\begin{array}{l}{y=x+3①}\\{7x+5y=9②}\end{array}\right.$
把①代入②得:7x+5(x+3)=9,
解得:x=-$\frac{1}{2}$,
把x=-$\frac{1}{2}$代入①得:y=-$\frac{1}{2}$+3=$\frac{5}{2}$,
所以原方程组的解为:$\left\{\begin{array}{l}{x=-\frac{1}{2}}\\{y=\frac{5}{2}}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{3s-t=5①}\\{5s+2t=15②}\end{array}\right.$
①×2+②得:11s=25,
解得:s=$\frac{25}{11}$,
把s=$\frac{25}{11}$代入①得:$\frac{75}{11}$-t=5,
解得:t=$\frac{20}{11}$,
所以原方程组的解为:$\left\{\begin{array}{l}{s=\frac{25}{11}}\\{t=\frac{20}{11}}\end{array}\right.$;
(3)$\left\{\begin{array}{l}{4x+y=15①}\\{3x-2y=3②}\end{array}\right.$
①×2+②得:11x=33,
解得:x=3,
把x=3代入①得:12+y=15,
解得:y=3,
所以原方程组的解为:$\left\{\begin{array}{l}{x=3}\\{y=3}\end{array}\right.$;
(4)整理得:$\left\{\begin{array}{l}{4x+5y=-7①}\\{2x+3y=-3②}\end{array}\right.$
①-②×2得:-y=-1,
解得:y=1,
把y=1代入②得:2x+3=-3,
解得:x=-3,
所以原方程组的解为:$\left\{\begin{array}{l}{x=-3}\\{y=1}\end{array}\right.$.
点评 本题考查了解二元一次方程组的应用,能把二元一次方程组转化成一元一次方程是解此题的关键.

 如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:
如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法: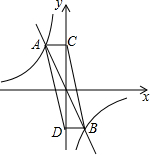 如图,直线y=kx(k<0)与双曲线y=$\frac{-2}{x}$交于点A、B,AC⊥y轴于C,BD⊥y轴于D,连接AD、BC,则四边形ABCD的面积为( )
如图,直线y=kx(k<0)与双曲线y=$\frac{-2}{x}$交于点A、B,AC⊥y轴于C,BD⊥y轴于D,连接AD、BC,则四边形ABCD的面积为( )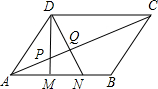 如图,在平行四边形ABCD中,M、N为AB的三等分点,DM、DN分别交AC于P、Q两点,则AP:PC=1:3,AP:PQ:CQ=5:3:12.
如图,在平行四边形ABCD中,M、N为AB的三等分点,DM、DN分别交AC于P、Q两点,则AP:PC=1:3,AP:PQ:CQ=5:3:12.